Otimização: aplicando programação não linear
Otimização unidimensional irrestrita - Apresentação
Olá! Me chamo Allan Spadini irei te acompanhar neste curso sobre Otimização: programação não-linear.
Audiodescrição: Allan Spadini é um homem de pele clara, com o rosto e lábios finos, cabelos e olhos castanhos. Veste uma camiseta preta lisa. Está em um estúdio com uma combinação de luzes verdes e azuis ao fundo.
O que vamos aprender?
Judecir Cavalcante desenvolveu este projeto para o curso, onde exploraremos a otimização dos lucros de uma companhia aérea. Após concluir o curso, você estará apto a resolver problemas de otimização não linear com as bibliotecas SciPy e Pyomo.
Pré-requisitos
Para acompanhar o conteúdo do curso, é necessário ter conhecimento em Python e em problemas de programação linear.
Espero você nos próximos vídeos do curso. Até lá!
Otimização unidimensional irrestrita - Entendendo o processo de precificação
Neste curso, vamos abordar a otimização dos lucros de uma companhia aérea. É possível que você já tenha se questionado sobre como é determinado o preço de uma passagem aérea, e talvez tenha percebido que esse preço costuma aumentar à medida que a data da viagem se aproxima.
Entendendo o cálculo do lucro
Aqui, exploramos o cálculo do lucro para a nossa companhia aérea:

O lucro é determinado multiplicando a quantidade de passagens aéreas vendidas pela tarifa, ou seja, o preço da passagem aérea. Contudo, é válido questionar se o preço da passagem aérea também é afetado pela quantidade de passagens vendidas.
Por isso, essa quantidade pode ser expressa em uma equação mais abrangente que inclui alguns termos adicionais.
A quantidade de passagens aéreas vendidas é determinada pela expectativa de vendas, que é um termo pré-definido baseado em estudos sobre a quantidade típica de passagens que a companhia aérea costuma vender, multiplicado por um mais um fator chamado elasticidade. Esse fator representa o quanto a tarifa aérea está influenciando a quantidade de passagens vendidas, sendo essencialmente um peso atribuído à tarifa aérea.
Também teremos a tarifa original dentro dessa fórmula, que também é um termo pré-determinado, que pode ser feito através de um estudo, qual é a tarifa inicial que vamos aplicar ao problema.
Para o nosso problema, vamos assumir que a expectativa de vendas e a tarifa original são constantes. Esses valores são pré-determinados, assumimos que para o nosso problema, teremos o valor de 388 para a expectativa de vendas e o valor de 500 para a tarifa original.
A elasticidade vamos assumir também que é uma incógnita. Ou seja, iremos assumir que ela é uma constante, que ela pode variar de dia para dia, mas por enquanto não vamos especificar um valor para a elasticidade.
Implementando a equação
Queremos começar implementando no Google Colab a nossa equação da quantidade de passagens aéreas vendidas para verificar como serão os valores aplicados quando substituímos a tarifa e o valor de elasticidade.
Criaremos a função estimar_demanda(). A demanda será um outro nome que vamos dar para a quantidade no nosso problema. Em uma célula, digitamos a seguinte equação:
def estimar_demanda(tarifa, elasticidade):
quantidade = 388 * (1 + elasticidade) * (500 - tarifa) / 500)
return quantidade
Teclamos "Shift + Enter" para rodar a célula. Agora, conseguimos calcular o lucro, porque o lucro depende dessa quantidade.
Em uma nova célula, inserimos o def estimar_lucro(tarifa, elasticidade). Na linha seguinte, passamos que a quantidade é igual a função estimar_demanda(tarifa, elasticidade). Na sequência, passamos que o lucro é igual à quantidade vezes a tarifa e retornamos o lucro.
def estimar_lucro(tarifa, elasticidade):
quantidade = estimar_demanda(tarifa, elasticidade)
lucro = quantidade * tarifa
return lucro
Rodamos com "Shift + Enter".
Agora, teremos constantes que serão definidas para esse problema, para facilitar o cálculo, sendo valores fictícios que serão adotados para a tarifa e para a elasticidade.
Adotaremos uma tarifa de 580, ligeiramente diferente do valor original de 500. Como estamos próximos à viagem, optamos por aplicar uma tarifa de 580. Dessa forma, qual será a demanda, isto é, a quantidade de passagens vendidas nesse cenário? Passamos também uma elasticidade que será igual a 0.1.
tarifa = 580 # Preço fixo
elasticidade = 0.1 # Elasticidade de preço fixa
Teclamos novamente "Shift + Enter".
Na célula seguinte, calculamos a demanda com a função estimar_demanda(tarifa, elasticidade).
demanda = estimar_demanda(tarifa, elasticidade)
Mais uma vez "Shift + Enter" para executar a célula. Na próxima célula, calculamos que o lucro será igual a função estimar_lucro().
lucro = estimar_lucro(tarifa, elasticidade)
Teclamos "Shift + Enter". Na célula seguinte, digitamos demanda e rodamos a célula.
demanda
Obtemos como retorno:
381.792
Podemos observar que a nossa demanda ficará aproximadamente em 381 unidades. Podemos considerar, por exemplo, uma demanda de 382 passagens aéreas vendidas. Digitamos lucro na célula seguinte e obtemos:
lucro
221439.36
O lucro para este caso, com essa demanda e com a tarifa de 580, seria de 221.439.
Conseguimos implementar e aplicar as duas funções. Um ponto crucial a ser observado aqui é que na função de lucro, temos uma relação não linear; ou seja, essa função não pode ser representada por uma reta. Nesse caso, temos um elemento desconhecido, nossa incógnita, que é a tarifa, a qual está multiplicando outro valor de tarifa. Isso se assemelha a um y sendo igual a x², por exemplo. Estamos lidando com uma equação quadrática nesse contexto.
Poderíamos ter outros problemas onde temos funções não lineares, como exponencial, uma função logarítmica. E todos esses problemas não lineares exigem aplicações de funções de otimização específicas. São justamente os problemas que vamos estudar nesse curso.
Próximos Passos
No próximo vídeo, porém, vamos estudar um pouco mais sobre o termo elasticidade. É um termo específico desse problema de precificação, que é um peso que vamos dar para o quanto que a tarifa está impactando na nossa quantidade de passageiros aéreos vendidos.
Até o próximo vídeo, onde vamos entender melhor o termo de elasticidade!
Otimização unidimensional irrestrita - Detalhando a função da expectativa de demanda
Antes de partirmos diretamente para o problema de otimização, vamos tentar entender como esse fator de elasticidade está impactando o problema.
Entendendo o fator de elasticidade
Para fazer isso e visualizar essa informação, vamos construir um gráfico que nos retornará a quantidade de passagens vendidas pela elasticidade.
Para isso, vamos construir o gráfico com a matplotlib e também precisaremos da biblioteca NumPy para criar os eixos do gráfico. Em uma célula, faremos o import da NumPy como np e depois o import da matplotlib.pyplot como plt.
import numpy as np
import matplotlib.pyplot as plt
Teclamos "Shift + Enter".
Agora, na célula seguinte vamos construir o eixo das elasticidades, o qual será definido como [], passando round(i, 2). Ainda dentro dos colchetes, inserimos for i in np.linspace(). Para o np.linspace(), usaremos os valores -0.5, 0.5 e 21 para obter as elasticidades desejadas.
elasticidades = [round(i, 2) for i in np.linspace(-0.5, 0.5, 21)]
Para rodar a célula, teclamos "Shift + Enter".
Em seguida, precisamos de uma tarifa fixa para nosso exemplo. Utilizaremos a função estimar_demanda() que foi desenvolvida no vídeo anterior para calcular as quantidades_vendidas. Então, vamos abrir e fechar colchetes, chamar a estimar_demanda(), abrir e fechar parênteses, passar a tarifa , elasticidade.
Ainda dentro dos colchetes, criamos um loop for para percorrer cada uma das elasticidades da nossa lista para passá-las para essa função. Então, vamos fazer o for elasticidade in elasticidades.
quantidades_vendidas = [estimar_demanda(tarifa, elasticidade) for elasticidade in elasticidades]
Agora temos as quantidades vendidas e as elasticidades.
Na sequência, inserimos plt.plot(), passando a elasticidades, quantidades_vendidas e vamos plotar esse gráfico teclando "Shift + Enter".
plt.plot(elasticidades, quantidades_vendidas)
Apenas para estilizar o gráfico, vamos copiar aqui uma informação para termos o nosso eixo x e eixo y escritos.
plt.plot(elasticidades, quantidades_vendidas)
plt.xlabel('Elasticidade de Preço')
plt.ylabel('Quantidade de Tickets Vendidos')
plt.title('Impacto da Elasticidade no Número de Tickets Vendidos')
plt.legend()
plt.grid(True)
Teclamos "Shift + Enter".
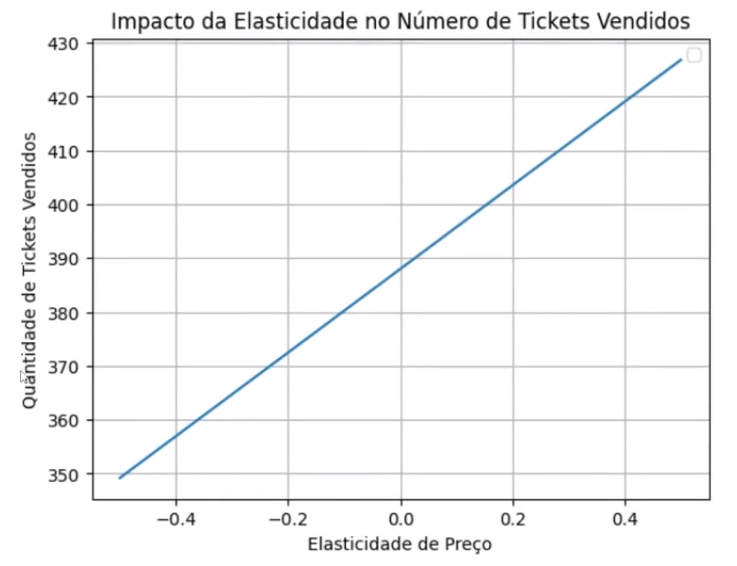
No eixo y temos a quantidade de passagens vendidas e no eixo x temos a elasticidade de preço.
Lembre-se que adotamos um valor fixo da tarifa. Para esse nosso estudo, observamos que para um fator de elasticidade de preço igual a zero, a elasticidade está dizendo que o valor da tarifa não tem um peso em relação à quantidade de passagens vendidas.
Esse seria o caso que ela não tem um peso para a elasticidade de valor igual a zero. Se tivermos um valor de elasticidade maior do que zero, isso significa que o valor da quantidade de passagens vendidas, será maior do que o valor pré-definido, de 388, que era o valor inicial que estávamos esperando. Por outro lado, se a elasticidade for negativa, teremos um valor mais baixo de quantidade de passagens vendidas.
Esse valor de elasticidade precisa ser pré-determinado em relação ao nosso problema. Mas para continuar entendendo um pouco mais o problema, vamos construir outro gráfico que nos mostrará o mapa de calor da elasticidade e da tarifa.
Mapa de calor da elasticidade e tarifa
Para construir esse gráfico, precisaremos inverter a ordem do eixo Y, que será o eixo da elasticidade, porque desejamos exibir o valor variando do menor para o maior. Para isso, vamos utilizar o termo elasticidades = elasticidades[::-1], isso vai inverter nosso eixo.
elasticidades = elasticidades[::-1]
Teclamos "Shift + Enter".
Criamos também um eixo de tarifas. Então, vamos passar tarifas = np.arange(400,600,10).
tarifas = np.arange(400,600,10)
Agora vamos criar as demandas esperadas novamente, mas como uma matriz, que vamos visualizar no mapa de calor. Para isso, começamos preenchendo essa matriz com zeros, criamos na célula seguinte demandas_esperadas = np.zeros((len(elasticidades), len(tarifas))).
demandas_esperadas = np.zeros((len(elasticidades), len(tarifas)))
Na sequência, criamos um loop for para preencher essa matriz.
Logo após, construímos nosso loop for, então for i, elasticidade in enumerate(elasticidades): e depois outro loop for, for j, tarifa_fixa in enumerate(tarifas):. Na linha seguinte, inserimos demanda_esperada = estimar_demanda(tarifa_fixa, elasticidade) e na linha de baixo vamos preencher a nossa matriz efetivamente, demandas_esperadas[i, j] = demanda_esperada.
for i, elasticidade in enumerate(elasticidades):
for j, tarifa_fixa in enumerate(tarifas):
demanda_esperada = estimar_demanda(tarifa_fixa, elasticidade)
demandas_esperadas[i, j] = demanda_esperada
Teclamos "Shift + Enter".
Agora, conseguimos construir nosso mapa de calor.
Faremos primeiro a importação com import seaborn as sns.
import seaborn as sns
Agora, iremos construir o heatmap (mapa de calor) com sns.heatmap(demandas_esperadas, cmap='RdYlGn'). Basicamente, estamos passando aqui esse valor de demandas esperadas para preencher o mapa de calor. Irei colar alguns critérios para a estilização do gráfico.
sns.heatmap(demandas_esperadas, cmap='RdYlGn', xticklabels=tarifas, yticklabels=elasticidades)
plt.xlabel('Tarifa')
plt.ylabel('Elasticidade de Preço')
plt.title('Demanda Esperada em um Gráfico de Calor')
plt.show()
Teclamos "Shift + Enter" e obtemos:
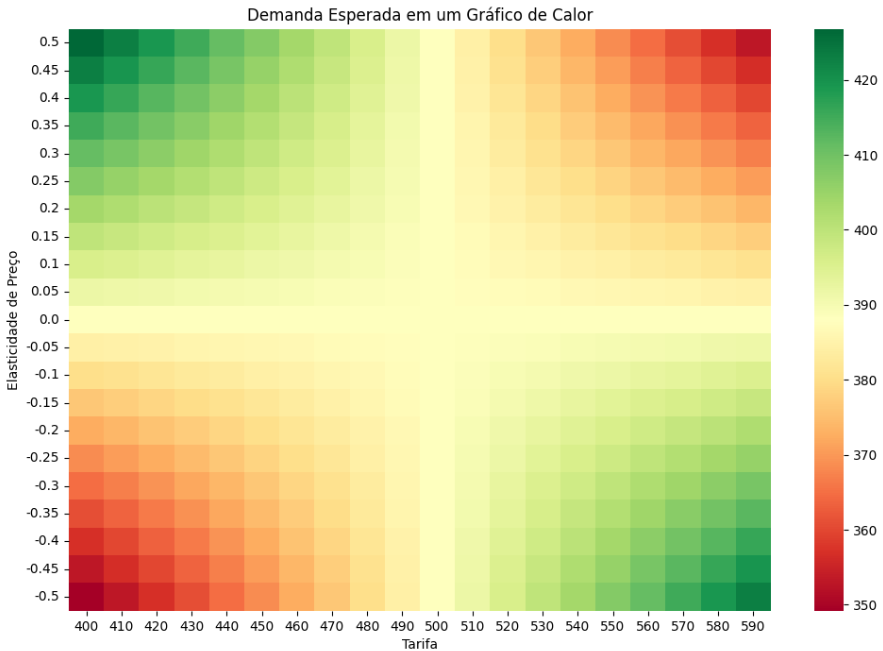
Qual é a informação transmitida por este mapa de calor? Ele indica que para diferentes níveis de tarifa e elasticidade de preço, haverá uma correspondente quantidade de passagens vendidas.
Nós interpretamos a cor neste contexto como representando a quantidade de passagens vendidas. Assim, as várias combinações de elasticidade, preço e tarifa nos fornecem insights sobre o comportamento esperado da demanda.
Esse é um tipo de gráfico que seria utilizado em um estudo pré-realizado sobre esse problema, sobre qual elasticidade de preço, como a elasticidade de preço será aplicada na nossa equação.
Para efeitos de aplicação prática, vamos assumir que a elasticidade de preço é um fator pré-determinado e fixo, para um determinado dia do nosso problema. Então vamos assumir que estamos começando trabalhando com um único dia, então teremos um único valor para determinado dia de elasticidade.
Como mencionamos, essa elasticidade é um fator específico da precificação da passagem aérea, e se você tiver curiosidade de entender melhor como ele funciona, terá uma atividade em texto para você ver como esse fator implica no nosso cálculo da precificação das passagens aéreas.
Próximos Passos
No próximo vídeo, vamos retornar à equação do lucro e vamos fazer o processo de otimização. Iremos escolher a tarifa que nos retorna o melhor lucro possível, assumindo que seremos constantes para todos os outros fatores dessa fórmula.
Até o próximo vídeo!
Sobre o curso Otimização: aplicando programação não linear
O curso Otimização: aplicando programação não linear possui 116 minutos de vídeos, em um total de 44 atividades. Gostou? Conheça nossos outros cursos de Machine Learning em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- Otimização unidimensional irrestrita
- Otimização unidimensional restrita
- Otimização multidimensional irrestrita
- Otimização multidimensional restrita
- Solvers de otimização não-linear