Pesquisa operacional: entendendo as bases dos métodos de otimização
Conhecendo o problema e a força bruta - Apresentação
Você faz muitas compras online? Aposto que bem perto de você deve ter um item que você encomendou recentemente e chegou na sua casa. Você já refletiu sobre a logística por trás das entregas? Ou seja, quais decisões as empresas tomaram para que aquele item chegasse à sua casa dentro do prazo correto?
Olá, sou Judecir Cavalcante e serei seu instrutor nesse curso de pesquisa operacional, onde vamos explorar análise prescritiva e otimização.
Audiodescrição: Judecir é um homem branco com olhos castanhos e cabelo curto, liso e escuro. Usa óculos de armação quadrada e preta e um headphone também preto. Está com uma camisa cinza. Ao fundo, uma parede na cor de gelo sem decorações.
O que vamos aprender?
Este curso é destinado a quem deseja ampliar os horizontes no mundo de ciência de dados, portanto, vamos aprender sobre métodos que auxiliam na tomada de decisão.
Vamos focar no problema das entregas, imaginando que uma empresa tem um caminhão que parte de um centro de distribuição e deve passar por vários endereços, realizando diversas entregas. E, por fim, esse caminhão deve ser direcionado para um destino final, ou seja, uma oficina.
Após este curso, você será capaz de avaliar os principais métodos para a tomada de decisão, saber quando usar qual abordagem e será capaz de auxiliar na tomada de decisão de problemas mais complexos.
Pré-requisitos
Este curso é para quem está começando na área, logo, vamos solicitar o básico da linguagem Python para que você possa acompanhar as implementações e, claro, criar a sua própria versão.
Você se interessou em como a pesquisa operacional pode auxiliar na tomada de decisão e na resolução de problemas complexos? Se sim, te aguardamos no próximo vídeo!
Vamos juntos nessa jornada. Até mais!
Conhecendo o problema e a força bruta - O problema das entregas: origem, endereços e destino
Você costuma fazer muitas compras pela internet? Com que frequência recebe produtos em sua casa, seja um livro ou uma blusa comprada recentemente?
Da próxima vez que receber uma encomenda, pense um pouco na logística por trás da entrega. Estamos falando especificamente do tipo de problema que vamos mostrar agora.
Pesquisa operacional
Imagine um ponto de origem, que pode ser um centro de distribuição ou a própria loja. Há uma equipe responsável pelas entregas que vai sair e passar por vários endereços, chegando em um outro destino no final. Este pode ser um outro centro de distribuição ou até uma oficina para a manutenção do caminhão.
Podemos nos perguntar, como será que essa decisão é tomada?
Quem toma essa decisão? Será que é a pessoa que dirige o caminhão que vai decidir qual é a melhor rota? Ou será que tem um time por trás planejando a maneira mais adequada de tomar essa decisão?
E com que objetivos? Queremos economizar custos ou fazer o trajeto em uma distância menor? Um objetivo razoável é exatamente tentar percorrer essa rota de uma maneira que economize tempo. Ou seja, tentar percorrer a menor distância possível.
Imagine um exemplo, onde estamos percorrendo uma rota específica. Teríamos um ponto em azul de origem, vários pontos em vermelho que representam os endereços e um ponto em verde que é o destino final.
Neste exemplo, teríamos um custo total de 24 km percorridos. No entanto, talvez ao alterar a rota - a ordem em que visitamos os vértices, os endereços - seja possível obter um ganho de 1 km. Esse quilômetro pode ser entendido como, em primeiro lugar, distância e, em seguida, como uma redução de custos.
A pesquisa operacional surge para solucionar esse tipo de problema de tomada de decisão, apontando qual a melhor maneira de fazer isso ou aquilo.
É isso que vamos explorar no curso, como tomar a decisão desse problema específico do roteamento de entregas de maneira a minimizar a distância.
Origem, endereços e destino
Para definir alguns conceitos, vamos partir de uma origem e chegar a um destino. Todos esses endereços que estamos considerando pelo caminho, vão ser representados como pontos do plano cartesiano. Ou seja, uma coordenada x e uma coordenada y.
Consideramos também a distância euclidiana, que basicamente é a linha reta entre dois pontos do plano.
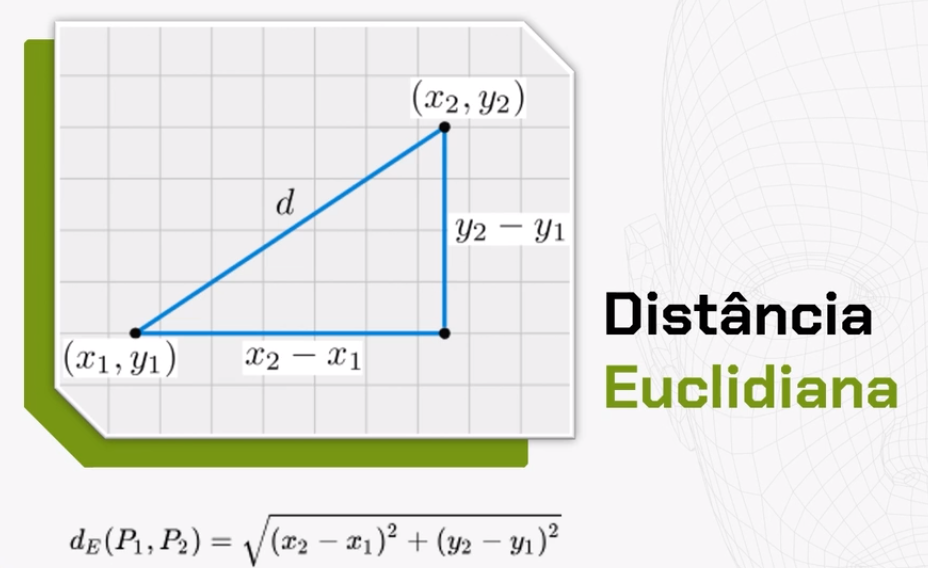
Antes de partirmos para a resolução desse problema com algoritmos robustos que conseguem encontrar a melhor decisão, vamos representar esse problema no Python. Identificar que estruturas de dados e funções podem nos auxiliar.
Vamos abrir o Google Colab. Preenchemos previamente uma origem, que vai ser uma tupla de onde estamos partindo: (0,0). Também definimos um destino, que é o objetivo final onde queremos chegar, também é uma tupla.
E uma lista de enderecos, onde cada elemento da lista vai ser uma tupla, que representa o endereço que precisamos visitar.
origem = (0,0)
destino = (4,4)
enderecos = [(2, 1), (2,2), (8, 3), (5, 3)]
Agora, podemos visualizar essa origem e esses destinos em um mapa para entender como eles estão distribuídos e começar a pensar na estratégia de resolução.
Além disso, podemos definir outra variável chamada rota. Vamos criar uma célula para defini-la. Ela será uma rota trivial, ou seja, uma rota super simples e intuitiva, só para conseguir representá-la e também desenhá-la no mapa para verificar como seriam essas primeiras explorações do problema.
Essa rota mais trivial que podemos pensar é basicamente partir da origem. Vamos colocar essa variável entre colchetes, porque vamos definir a rota como uma lista. Em seguida, vamos concatená-la com a nossa lista de endereços
E, por fim, concatenar com a nossa lista de destinos. No caso, colocamos variável destino entre colchetes para transformá-la em uma lista.
rota = [origem] + enderecos + [destino]
Assim, vamos nos mover da origem para o primeiro ponto da lista de endereços, depois para o segundo e assim sucessivamente até chegarmos ao destino. Executaremos as duas células usando "Shift + Enter".
A execução do código pode demorar um pouco, pois o Colab está alocando nosso recurso. Enquanto ele conecta e executa, inspecionaremos o objeto rota para verificar como ele se formou.
rota
[(0,0), (2,1), (2,2), (8,3), (5,3), (4,4)]
Note que o resultado é uma concatenação de todos os pontos que temos.
Agora, podemos implementar a visualização desta rota. Para isso, podemos importar uma biblioteca do Python chamada matplotlib. Em uma nova célula, vamos escrever:
import matplotlib.pyplot as plt
A biblioteca Matplotlib é amplamente conhecida na área de dados, utilizada para realizar visualizações em análises exploratórias e afins. Google Colab já entende que essa é a importação que queremos fazer. Executamos o comando usando "Shift + Enter".
Agora, também podemos importar a biblioteca que calculará a nossa distância euclidiana. A distância entre dois pontos do nosso problema será representada pela distância euclidiana. Para isso, podemos usar a biblioteca SciPy.
Basta escrever from scipy.spatial.distance. Nesse caminho, vamos importar a distância euclidean com um nome diferente, escrevendo import euclidean as distancia_euclidiana. Com isso, damos um apelido mais intuitivo para essa distância em específico.
from scipy.spatial.distance import euclidean as distancia_euclidiana
Com as ferramentas necessárias importadas, podemos começar a desenhar o nosso gráfico. Podemos começar definindo uma variável que será o tamanho dessa lista de rotas. Vamos chamá-la de tamanho_rota e ela será igual a len(rota), ou seja, o número total de elementos que temos.
tamanho_rota = len(rota)
Em seguida, podemos criar um loop for i in range (tamanho_rota) para percorrer todos os índices da nossa lista de rotas com a origem, endereços e destino. Após acrescentar dois-pontos e "Enter", queremos plotar cada ponto em rota.
Podemos fazer um plt.scatter() para criar um gráfico de dispersão da rota[i].
for i in range(tamanho_rota):
plt.scatter(rota[i])
TypeError: scatter() missing 1 required positional argument: 'y'
Se executamos, observe que o scatter() pede dois parâmetros, x e y. Em vez de chamar plt.scatter(rota[i]), vamos passar x e y. Antes da definição, vamos dizer que x e y serão iguais a rota[i]. Isso significa que estamos armazenando em x e y as coordenadas dessa posição do vetor de rota.
for i in range(tamanho_rota):
x, y = rota[i]
plt.scatter(x, y)
Ao executar novamente as células, teremos um gráfico. Mas note que ele é plotado com várias cores diferentes, dificultando a identificação de quem é a origem, quem é o destino e quem é um endereço.
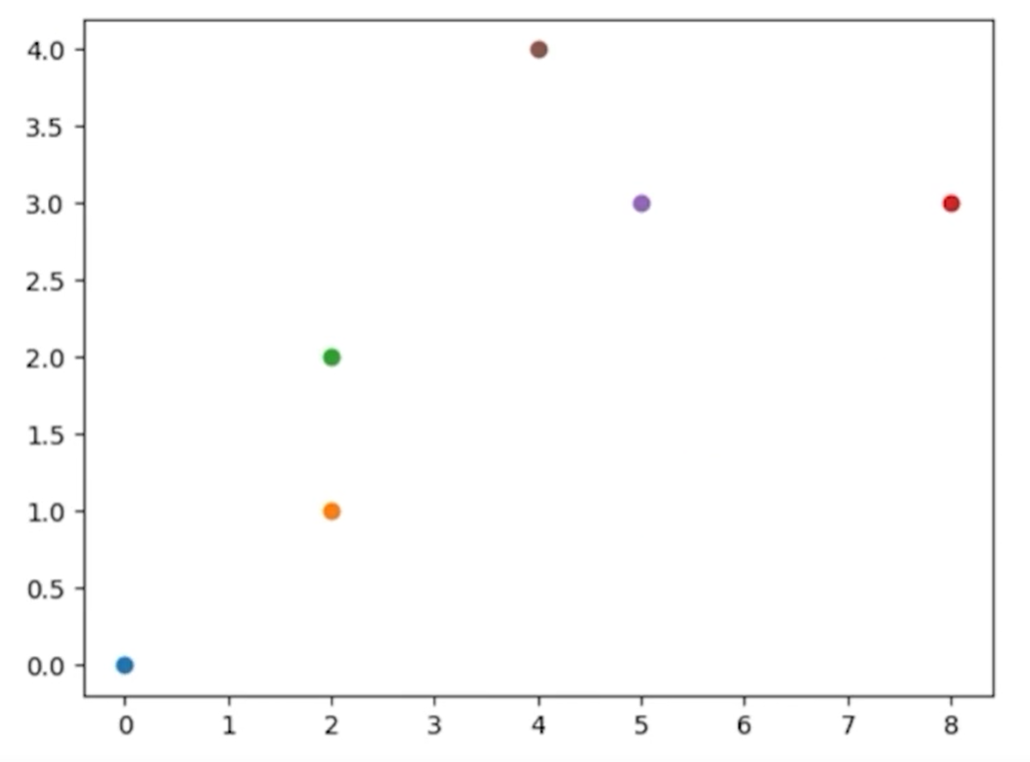
Para resolver isso, podemos passar uma variável color igual à cor como parâmetro do scatter(). Inicialmente, vamos definir a variável cor como black, ou seja, preta.
No entanto, ao fazer isso, todos os pontos do gráfico serão pintados de preto. Porém, precisamos distinguir quem é a origem e quem é o destino, para que possamos entender claramente o ponto de partida, quais são os endereços a serem visitados para fazer as entregas e onde precisamos chegar.
Para resolver isso, podemos alterar o valor da variável cor dependendo em que posição da lista rota estamos.
Então, podemos fazer o seguinte: se i for igual a zero, ou seja, se estivermos no primeiro ponto, podemos definir a cor como blue. Isso significa que o ponto de origem será representado pela cor azul.
Caso contrário, vamos dar um "Enter" e identar fora do if. Podemos criar uma condição "senão se", isto é, elif onde i é igual à tamanho_rota substraído de 1. Ou seja, estamos na última posição da lista rota. Essa é exatamente a posição onde o destino estará. Nesse caso, podemos configurar a cor para ser igual a red, ou seja, vermelho.
E se não for nenhum dos dois, não queremos fazer nada, podemos manter a cor como preto.
for i in range(tamanho_rota):
x, y = rota[i]
cor = "black"
if i == 0:
cor = "blue"
elif i == tamanho_rota - 1:
cor = "red"
plt.scatter(x, y, color=cor)
Agora, se executamos com "Shift+Enter", verificamos que conseguimos montar o gráfico adequadamente. A origem (0,0) está em azul, os pontos em preto são os pontos que precisamos visitar para fazer as entregas. No final, o ponto em vermelho no (4,4) será o nosso destino.
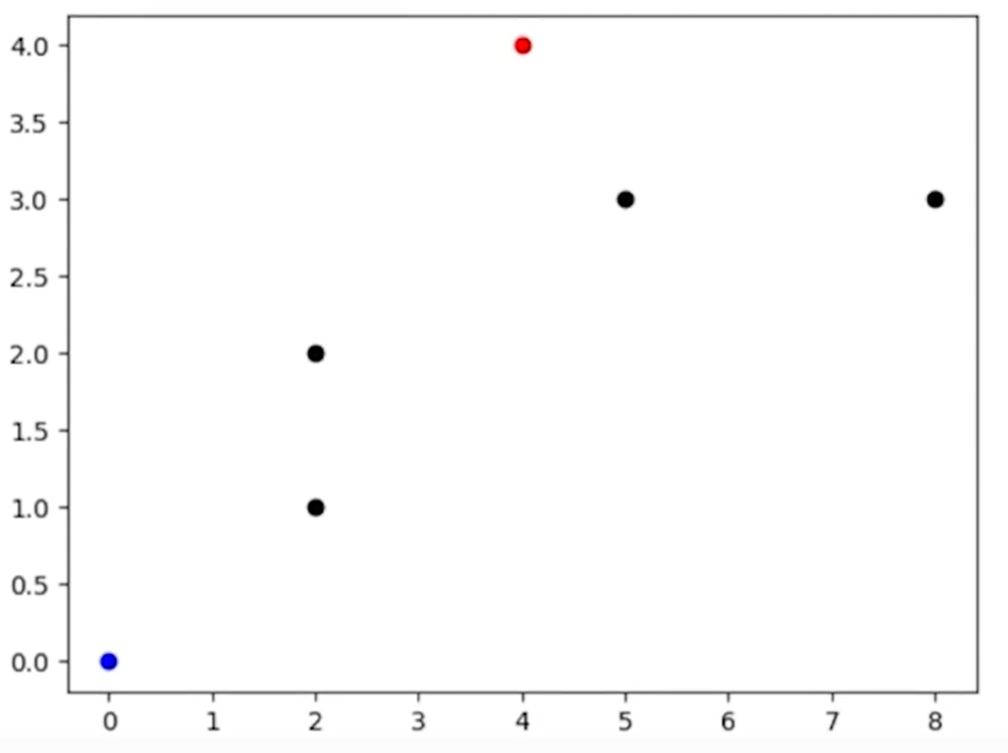
O que podemos fazer agora? Podemos adicionar uma seta de cada ponto para o próximo para indicar que aquele caminho está sendo seguido.
Do ponto azul, podemos criar uma seta apontando para (2,1) para indicar que a rota foi do ponto (0,0) para (2,1). Para fazer isso, usaremos o matplotlib.pyplot, utilizando uma função mais específica chamada plt.arrow.
Abaixo de plt.scatter(), vamos digitar plt.arrow(), passando x e y.
Agora, vamos mostrar a documentação da função arrow() no site do Matplotlib para descobrir algo interessante. A documentação nos informa que se queremos criar um gráfico de setas de x e y, os outros dois argumentos serão dx e dy. Ou seja, ele vai criar uma seta de x e y até x + dx e y + dy.
Portanto, se quisermos ir de um ponto para o outro, os dois últimos parâmetros dx e dy devem ser iguais à diferença desses pontos.
Vamos voltar para o Google Colab. Se quisermos ir para rota[i] + 1 (que seria a próxima posição do vetor i), temos que calcular anteriormente essas duas diferenças de coordenadas. Para isso, podemos chamar de x1, y1 as coordenadas da próxima posição de rota, ou seja, rota[i] + 1.
Em seguida, podemos calcular dx que será x1 - x e dy que será y1 - y.
Na função plt.arrow(), passamos x, y, dx e dy. Também podemos passar uma cor. Vamos definir a color como black para todos os casos.
E, por fim, o tamanho da seta que queremos marcar. Se não definirmos um tamanho para a seta, ela ficará sem nenhuma seta. Por isso, podemos fazer head_width igual a 0.1 para indicar que seu tamanho será 0.1.
x1, y1 = rota[i+1]
dx = x1 - x
dy = y1 - y
plt.arrow(x, y, dx, dy, color="black", head_width=0.1)
Vamos executar toda a célula para verificar o resultado.
IndexError: list index out of range
Perfeito! Ele tentou executar e fez algumas setas entre os pontos do gráfico, no entanto, recebemos um erro informando que tentamos acessar uma posição que não existe na nossa lista rota. Mas, por quê?
Porque como ele faz i + 1, percorrendo toda a lista, ele acaba, na última posição, tentando acessar uma posição que de fato não existe.
Para solucionar isso, podemos adicionar uma condição. Só queremos plotar a seta, se nós estamos na penúltima posição. Ou seja, antes de x1, y1 = rota[i+1], podemos fazer um if para verificar se i é menor do que len(rota) - 1 seguido por dois-pontos. Em seguida, vamos adicionar uma indentação no que está abaixo para que fique dentro do if.
if i < tamanho_rota - 1:
x1, y1 = rota[i+1]
dx = x1 - x
dy = y1 - y
plt.arrow(x, y, dx, dy, color="black", head_width=0.1)
Ou seja, se estamos na penúltima posição da lista, que é a tupla (5,3), nós queremos fazer a seta para (4,4). E quando estivermos na última posição (4,4), nós não queremos fazer mais setas, pois todas as setas necessárias já foram desenhadas.
Podemos executar novamente essa célula para desenhar o caminho da entrega.
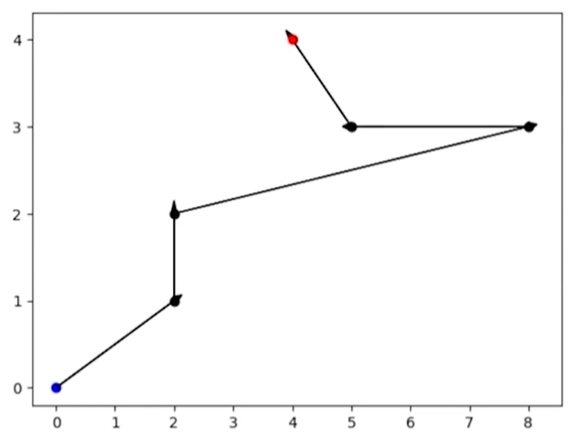
Para deixar o gráfico ainda mais completo, podemos calcular toda essa distância percorrida. Para isso, antes do for, podemos definir uma variável chamada distancia_percorrida e inicializá-la como zero. Assim, sempre que o for percorrer de um ponto para o outro, vamos acumular nessa variável a distância específica que percorremos.
distancia_percorrida = 0
Em outras palavras, o que queremos é somar a distancia_percorrida com a distancia_percorrida + distancia_euclidiana() de rota[i] para rota[i+1] dentro do if.
Isso deve ser feito dentro do if, porque só queremos acumular essa distância quando estivermos desenhando uma seta, ou seja, quando houver de fato um deslocamento. Então, quando chegarmos ao último ponto (ou seja, quando i for igual ao tamanho_rota - 1) não queremos acumular mais nada, porque já percorremos tudo o que era necessário.
Ao final do for, podemos fazer um print() do valor da distancia_percorrida.
for i in range(tamanho_rota):
# código omitido…
if i < tamanho_rota - 1:
x1, y1 = rota[i+1]
dx = x1 - x
dy = y1 - y
plt.arrow(x, y, dx, dy, color="black", head_width=0.1)
distancia_percorrida = distancia_percorrida + distancia_euclidiana(rota[i], rota[i+1])
print(distancia_percorrida)
Ao executar, teremos uma visualização do valor que percorremos:
13.733044070171104
Para deixar o gráfico bem informativo, podemos colocar esse valor de distancia_percorrida como o título do gráfico. Dessa forma, vamos saber tanto a rota que percorremos, como o custo dela.
Para isso, podemos adicionar plt.title() antes do print e usar uma f-string para formatar um título passando essa distância no título. Basta escrever f com aspas duplas e escrever a string Rota com distância de {distancia_percorrida}. Nesse caso, usamos chaves {} para passar uma variável ou um cálculo do Python dentro da f-string.
plt.title(f"Rota com distancia de {distancia_percorrida}")
Ao executar, o gráfico será plotado adequadamente, mas o valor da distância irá conter muitas casas decimais. Isso talvez não seja visualmente interessante, portanto, podemos arredondar distancia_percorrida dentro do plt.title() usando a função round().
Podemos fazer round(distancia_percorrida, 2) para dizer que só queremos mostrar as duas primeiras casas decimais. No final, ao invés do print(), podemos usar plt.show(), para mostrar o gráfico e não precisar retornar nenhum objeto dele.
Confira o código completo:
tamanho_rota = len(rota)
distancia_percorrida = 0
for i in range(tamanho_rota):
x, y = rota[i]
cor = "black"
if i == 0:
cor = "blue"
elif i == tamanho_rota - 1:
cor = "red"
plt.scatter(x, y, color=cor)
if i < tamanho_rota - 1:
x1, y1 = rota[i+1]
dx = x1 - x
dy = y1 - y
plt.arrow(x, y, dx, dy, color="black", head_width=0.1)
distancia_percorrida = distancia_percorrida + distancia_euclidiana(rota[i], rota[i+1])
plt.title(f"Rota com distancia de {round(distancia_percorrida, 2)}")
plt.show()
Ao executar, o gráfico será plotado adequadamente, mostrando o ponto de origem (que é o ponto em azul), percorrendo todos os endereços e chegando até nosso destino final (que é o ponto em vermelho).
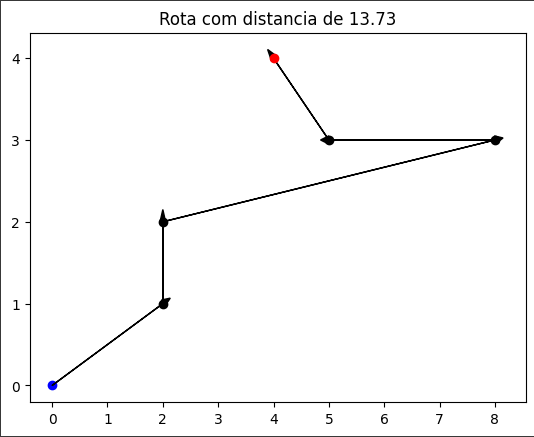
Próximos passos
Agora que compreendemos o problema e calculamos o custo total para uma solução trivial, estamos prontos para começar a implementar métodos de resolução.
Ou seja, devemos investigar qual a melhor solução que podemos adotar? Qual rota nos proporciona a menor distância total percorrida? É exatamente isso que vamos explorar nos próximos vídeos.
Conhecendo o problema e a força bruta - Resolução via força bruta
No último vídeo, aprendemos como estruturar o nosso problema, apresentando uma primeira visualização e calculando a distância total da rota. Agora, podemos começar a desenvolver estratégias para uma resolução.
Função para desenhar rota
Antes de iniciar, vamos transformar o código da aula anterior, que é responsável por desenhar o mapa e calcular a distância, em uma função.
Na última célula que criamos, podemos selecionar todo esse bloco de código, copiá-lo e na célula abaixo, podemos criar uma função def que pode ser denominada desenhar_rota. O parâmetro que essa função receberá a rota. Agora, colamos todo o código que tínhamos selecionado anteriormente.
Se as últimas linhas perderem a formatação, basta selecionar tudo novamente, exceto a primeira linha, e pressionar "Tab" para indentá-las novamente.
def desenhar_rota(rota):
tamanho_rota = len(rota)
distancia_percorrida = 0
for i in range(tamanho_rota):
x,y = rota[i]
cor = "black"
if i == 0:
cor = "blue"
elif i == tamanho_rota - 1:
cor = "red"
plt.scatter(x, y, color=cor)
if i < tamanho_rota - 1:
x1, y1 = rota[i+1]
dx = x1 - x
dy = y1 - y
plt.arrow(x, y, dx, dy, color="black", head_width = 0.1)
distancia_percorrida = distancia_percorrida + distancia_euclidiana(rota[i], rota[i+1])
plt.title(f'Rota com distancia de {round(distancia_percorrida, 2)}')
plt.show()
Executamos a célula com "Shift + Enter", criando nossa função.
Para testar, vamos copiar o código com os valores de exemplo de origem, destino e enderecos que definimos anteriormente, bem como o código referente a declaração da rota. Colamos na última célula criada e chamamos a nossa função desenhar_rota(), passando a rota.
origem = (0,0)
destino = (4,4)
enderecos = [(2,1), (2, 2), (8, 3), (5, 3)]
rota = [origem] + enderecos + [destino]
desenhar_rota(rota)
Executamos a célula com "Shift + Enter", a função realizará todos os cálculos e retornará o mesmo gráfico que criamos na aula anterior.
Vamos mudar um pouco agora. Em vez de seguir a rota padrão que define a origem em (0,0) e segue para (2,1), depois para (2,2) e assim por diante, vamos alterar essa ordem.
Neste momento, vamos supor que iremos iniciar pela tupla (2,2). Vamos dar um "Ctrl + X" nessa tupla e colá-la no início da nossa lista com o "Ctrl + V". Desse modo, alteramos a ordem do primeiro para o segundo ponto.
enderecos = [(2,2), (2, 1), (8, 3), (5, 3)]
Vamos executar com "Shift + Enter" e observar que a distância aumentou. Anteriormente era por volta de 13.73, mas agora subiu para 14.57.
Apesar de este resultado provavelmente não ser muito bom, o que pode-se notar é que, sempre que alteramos a ordem que passamos, obtemos uma nova rota e, consequentemente, uma nova distância.
Portanto, uma estratégia inicial que podemos considerar é enumerar todas as soluções possíveis e buscar qual é a melhor, ou seja, qual tem a menor distância.
Resolução via força bruta
Para enumerar todas as rotas possíveis, basicamente precisamos permutar, isto é, fazer todas as combinações possíveis de endereços. Para isso, há uma biblioteca no Python que já faz isso nativamente: a biblioteca Itertools.
Na célula abaixo, podemos dar um from itertools import permutations para importar esse módulo em específico. Vamos dar "Shift + Enter" para executar.
from itertools import permutations
Para ilustrar como será a permutação, faremos um for permutacao in permutations(), passando a lista de enderecos. A função permutations vai fazer todas as permutações de uma lista que passarmos para ela.
Dentro do for, vamos dar um print() em permutacao para escrevê-lo na tela.
for permutacao in permutations(enderecos):
print(permutacao)
Ao dar "Shift + Enter", ele gera todas as combinações possíveis de endereços.
- ((2,2), (2,1), (5,3), (8,3))
- ((2,2), (2,1), (8,3), (5,3))
- ((2,2), (5,3), (2,1), (8,3))
- ((2,2), (5,3), (8,3), (2,1))
- ((2,2), (8,3), (2,1), (5,3))
- restante omitido…
Perceba que a rota é a combinação de origem, a permutação e o endereço. Dentro do for, colocaremos que rota vai ser igual à origem entre colchetes para transformar em lista somado à permutacao somado ao destino também entre colchetes.
Porém, a permutacao não vem como uma lista por padrão, então é preciso convertê-la em uma lista. Para fazer isso, usamos o comando list(). Dessa vez, vamos imprimir a rota ao invés da permutacao.
for permutação in permutations(endereços):
rota = [origem] + list(permutacao) + [destino]
print(rota)
Ao executar novamente, o resultado é uma concatenação da origem, uma permutação específica e o destino.
- [(0,0), (2,2), (2,1), (5,3), (8,3), (4,4)]
- [(0,0), (2,2), (2,1), (8,3), (5,3), (4,4)]
- restante omitido…
Agora o que precisamos fazer é calcular essa distância percorrida. Nós já fizemos esse cálculo, mas está dentro da função de desenhar_rota(). Por isso, vamos precisar criar uma função para fazer isso.
Antes do for de permutacao, vamos criar uma nova célula. Nela, vamos definir uma função def chamada calcular_distancia_rota() que pode receber a rota específica.
Após os dois-pontos, em uma nova linha, vamos inicializar uma variável distancia que vai ser igual à zero. Em seguida, definimos a variável tamanho_rota como sendo o tamanho da lista, ou seja, len(rota).
Vamos fazer um for i in range() passando o tamanho_rota. De maneira similar ao vídeo anterior, queremos calcular a distância de rota da posição i para a posição i + 1, contanto que i não esteja na última posição, ou seja, se i for menor que tamanho_rota - 1.
Nesse caso, acumulamos na variável distancia. A distancia será igual à distancia + distancia_euclidiana() de rota[i] para rota[i+1].
No final do for, podemos retornar a distancia.
def calcular_distancia_rota(rota):
distancia = 0
tamanho_rota = len(rota)
for i in range(tamanho_rota):
if i < tamanho_rota - 1:
distancia = distancia + distancia_euclidiana(rota[i], rota[i+1])
return distancia
Vamos executar utilizando "Shift + Enter". Dentro do for permutacao, além da rota, vamos printar o calcular_distancia_rota(), passando a rota entre parênteses.
for permutação in permutations(endereços):
rota = [origem] + list(permutacao) + [destino]
print(rota, calcular_distancia_rota(rota))
- [(0,0), (2,2), (2,1), (5,3), (8,3), (4,4)] 14.557084025827841
- [(0,0), (2,2), (2,1), (8,3), (5,3), (4,4)] 14.567196007456046
- restante omitido…
Desse modo, conseguimos calcular a distância total percorrida para cada combinação de rota.
Agora, precisamos selecionar a menor rota. Mas, como fazemos isso?
Antes do for permutacao, precisamos definir uma variável chamada menor_distancia que começará como infinito, porque não sabemos ainda qual é ela. Podemos inicializar esta variável como float('inf'). Dessa maneira, indicamos ao Python que é uma distância muito grande, simbolizando infinito.
Também podemos definir uma variável menor_rota como None, pois também ainda não sabemos qual é.
menor_distancia = float('inf')
menor_rota = None
Depois de percorrer cada permutação e construir a rota, podemos salvar a distância dela em uma variável específica. Por isso, dentro do for, após rota, podemos fazer distancia_rota igual à calcular_distancia_rota(), passando a lista de rota.
Não vamos querer mais imprimir na tela, pois podem ser muitas combinações. Por isso, vamos apagar a linha com o print().
Agora, precisamos checar se essa rota específica é a menor que já tivemos, usando a condicional if. Se a distancia_rota for menor que a menor_distancia, atualizamos nossas variáveis de controle. Por isso, vamos dizer que menor_distancia vai ser igual à distancia_rota e, consequentemente, a menor_rota vai ser igual à rota que acabamos de encontrar.
No final do for, podemos imprimir a menor_rota e a menor_distancia. Além disso, também podemos chamar a função desenhar_rota() que criamos anteriormente, passando a menor_rota.
for permutacao in permutations(enderecos):
rota = [origem] + list(permutacao) + [destino]
distancia_rota = calcular_distancia_rota(rota)
if distancia_rota < menor_distancia:
menor_distancia = distancia_rota
menor_rota = rota
print(menor_rota, menor_distancia)
desenhar_rota(menor_rota)
Vamos executar no "Shift + Enter" para verificar se realmente encontrou a menor rota possível.
[(0,0), (2,1), (2,2), (5,3), (8,3), (4,4)] 13.52145126328583
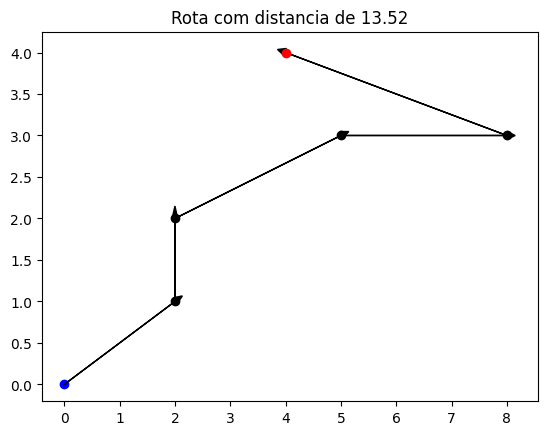
Perfeito, o algoritmo, também conhecido como Força Bruta ou Busca por Exaustão, encontrou a menor rota possível. Esta rota tem uma distância total percorrida de 13,52.
Próximo passo
Construímos o nosso primeiro método de resolução do problema das entregas para uma rota de origem, destino e origem. Este método, conhecido como método de Busca por Exaustão ou Força Bruta, busca todas as possíveis soluções dentro do for e retorna a de menor distância percorrida. Portanto, conseguimos otimizar o nosso problema.
Contudo, se adicionamos mais endereços, será que esse método continuará com um bom desempenho e conseguirá encontrar a solução? Vamos explorar essa questão em seguida.
Sobre o curso Pesquisa operacional: entendendo as bases dos métodos de otimização
O curso Pesquisa operacional: entendendo as bases dos métodos de otimização possui 188 minutos de vídeos, em um total de 65 atividades. Gostou? Conheça nossos outros cursos de Data Science em Data Science, ou leia nossos artigos de Data Science.
Matricule-se e comece a estudar com a gente hoje! Conheça outros tópicos abordados durante o curso:
- Conhecendo o problema e a força bruta
- Métodos heurísticos e meta-heurísticos
- Conhecendo os algoritmos em grafos
- Trabalhando com modelagem matemática
- Combinação de métodos e detalhes solução