Desvendando a Regressão Linear

Não importa se você é uma pessoa novata ou mais experiente no mundo dos dados, mas é bem provável que já tenha ouvido falar da famosa regressão linear ou tenha ajustado uma reta para visualizar a relação entre dois fenômenos. Mas, cá entre nós, como esse algoritmo funciona? Ou ainda, o que acontece por trás da previsão de dados quando utilizamos essa técnica?
A regressão linear simples é uma metodologia que estuda a relação entre dois fenômenos, permitindo entender o efeito e a causalidade entre eles, além de prever novos valores. Para compreender melhor, vamos desvendar como ajustar a reta, interpretar e prever valores.
Ajustando a reta
A relação entre dois fatores é estudada pela regressão linear simples através de uma fórmula que desenha uma reta. Para entender melhor essa relação usaremos um dos estudos do economista John Keynes. Ele concluiu que os indivíduos tendem a aumentar o seu consumo conforme sua renda aumenta. Essa é uma versão simplificada da função de consumo também estudada no curso de Estatística com R: Correlação e regressão.
Na tabela abaixo, podemos visualizar as cinco primeiras observações do conjunto de dados que utilizaremos:
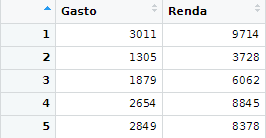
Podemos criar uma relação entre gasto e renda da seguinte forma:
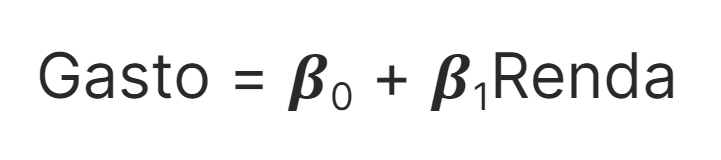
Aqui, cada componente representa um conjunto de valores, sendo:
- Gasto: gasto ou consumo das famílias
- Renda: renda disponível
- 𝜷0: consumo quando o rendimento é zero
- 𝜷1: propensão marginal a consumir
Usando o conjunto de dados como exemplo, essa função desenha a seguinte reta Gasto = 207.9 + 0.3Renda + erro:
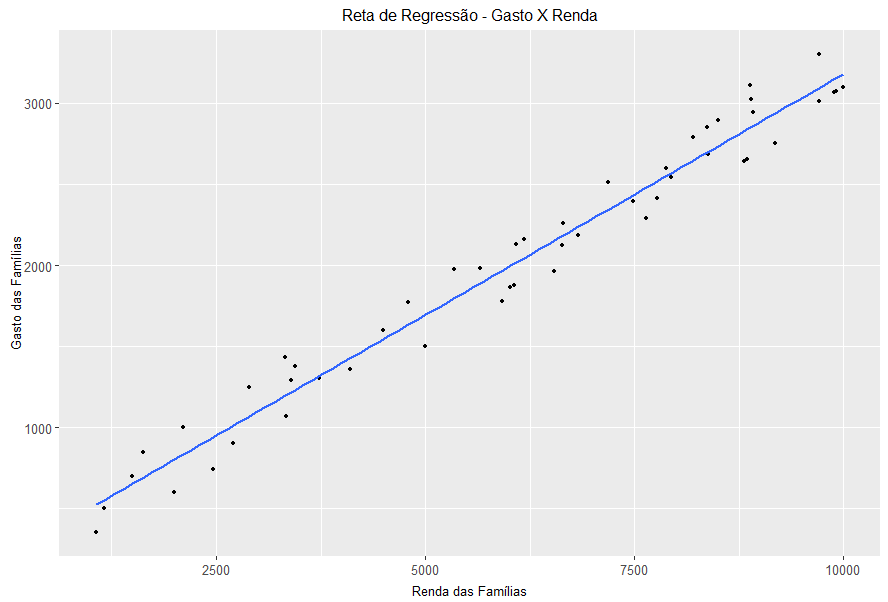
Podemos perceber que quanto menor a renda (X) menor é o gasto das famílias (Y). Ao centro, há uma nuvem de pontos na qual foi ajustada uma reta linear crescente que nos permite entender o comportamento médio dos gastos familiares. Mas, como passamos da função Gasto = 𝜷0+ 𝜷1Renda + erro para Gasto = 207.9 + 0.3Renda + erro?
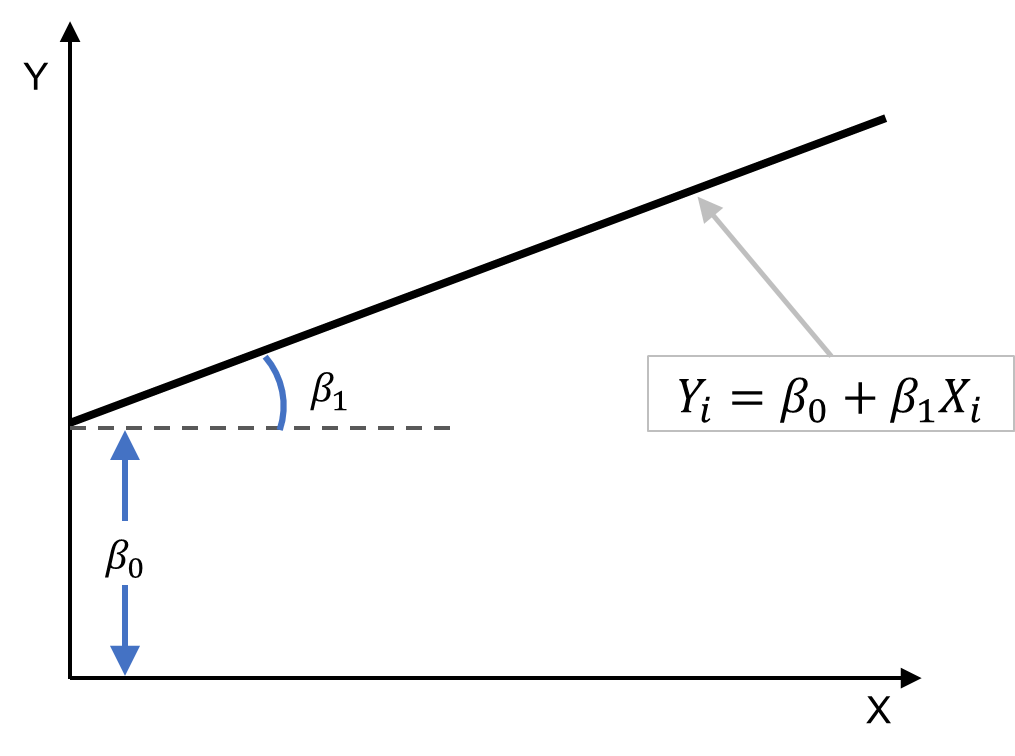
Independente do seu conjunto de dados, será ajustada uma reta que genericamente podemos representar pela função abaixo:
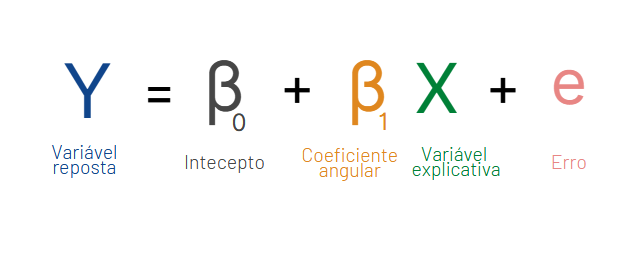
Y é o conjunto de valores que depende de uma explicação e X é a variável independente e explicativa. No nosso exemplo, o gasto da família depende da sua renda. O 𝜷0 também chamado de intercepto é o valor de Y quando o 𝑋i é zero. Já o 𝜷1, o coeficiente angular, nos informa a taxa de variação e o quão inclinada nossa reta será apresentada.
Ambos os parâmetros, 𝜷0 e 𝜷1, são desconhecidos e precisam ser estimados. Aqui não iremos nos estender nesse assunto, mas saiba que um dos processos mais utilizados para estimação desses coeficientes é o método dos mínimos quadrados. Em resumo, esse método cria uma reta mais próxima possível dos valores disponíveis a qual a diferença entre o valor real de Y e o valor esperado é mínimo.
A partir dos nossos dados e desse processo de estimação, podemos calcular os betas com as seguintes fórmulas:
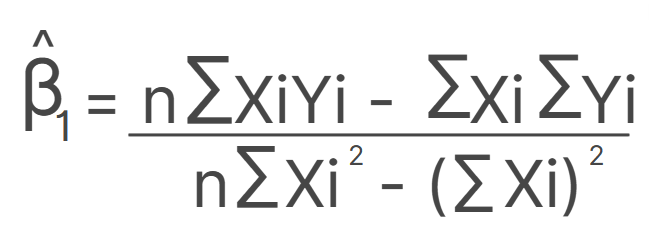
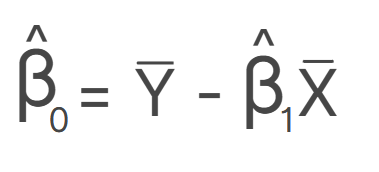
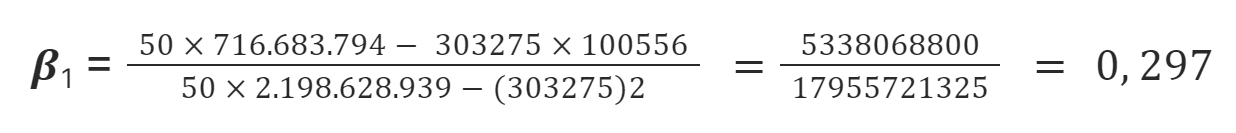
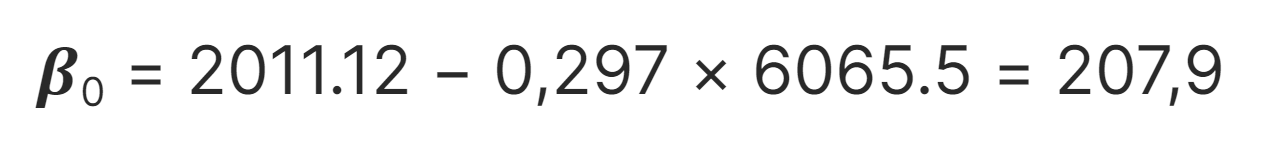
Formando:
Gasto = 207.9 + 0.3Renda + erroVocê deve ter percebido que nem todos os pontos estão alinhados na reta que ajustamos. Para isso, precisamos adicionar o erro na nossa fórmula, e, que é justamente a diferença entre o valor observado e o valor fornecido** pela equação.
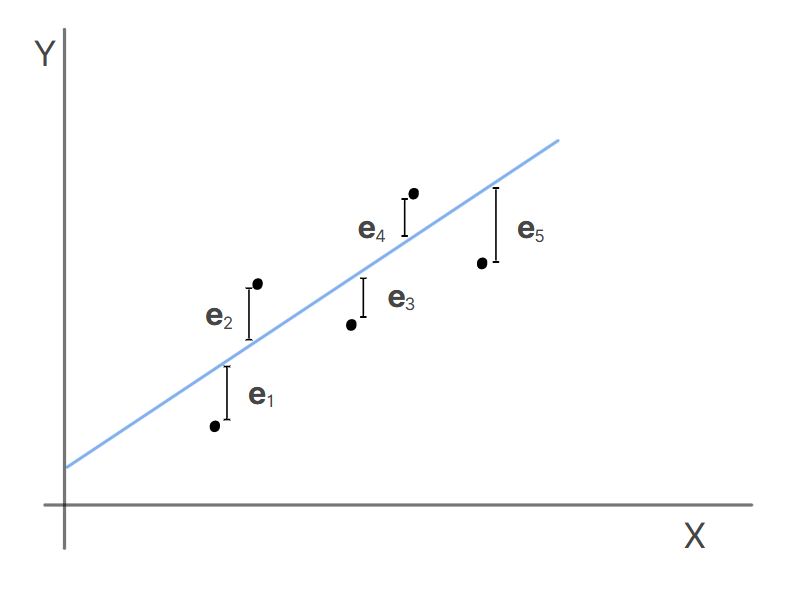
Agora que você já conheceu melhor todos os integrantes da regressão linear, é importante saber que a variável resposta (aquela que estamos tentando explicar e que depende de outros fatores), deve ser quantitativa, ou seja, deve apresentar valores numéricos.
No nosso caso, a variável resposta é o gasto familiar. Outros exemplos de variáveis são:

Se o que você procura estudar não estiver disposto em valores numéricos, capazes de tirar média e outras métricas, a regressão linear não é o método mais apropriado. Nesse caso, você poderá usar outras metodologias, como a regressão logística ou métodos de classificação.

Interpretando os valores
Você já ajustou a reta e também conhece cada um dos integrantes da nossa função. Vamos voltar ao exemplo e entender o que cada valor significa na prática?
Passamos de
Gasto = 𝜷0 + 𝜷1Renda + epara
Gasto = 207.9 + 0.3Renda + eNo nosso caso, 𝜷0 é 207,9, ou seja, o consumo (quando não há renda) é de 207,90 reais. Já o coeficiente relacionado à renda (𝜷1) indica que, a cada um real a mais na renda, o gasto médio esperado aumenta, em média, 0,30 reais. Dessa forma, quantifica-se o efeito da renda sobre o gasto.
Prevendo valores
Imagine que uma família possui renda de 3 mil reais, quanto seria o gasto estimado segundo nosso modelo? Podemos substituir 3.000 na fórmula e obter um gasto esperado estimado de Gasto = 207,9 + 0,3*(3000) = 1107,9.
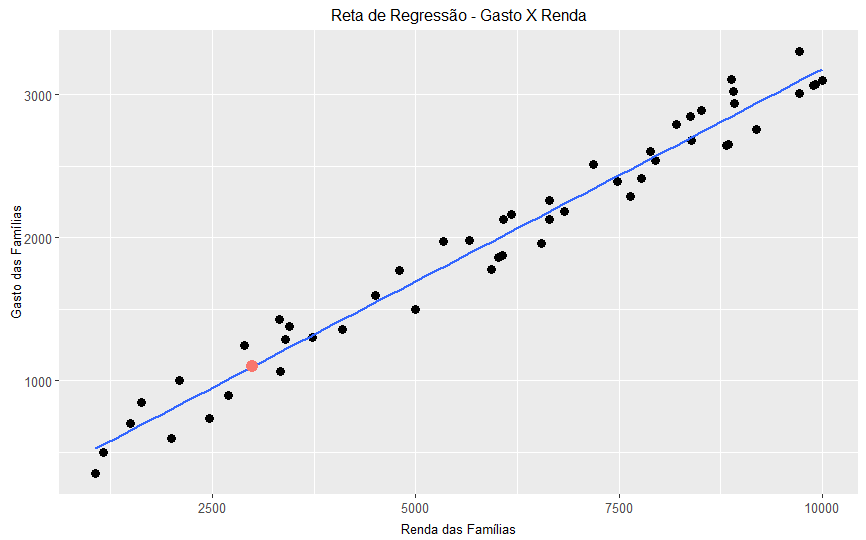
O ponto rosa no gráfico mostra nosso valor predito baseado na renda de três mil reais de renda familiar. Tenha em mente que a reta de regressão é capaz de quantificar a relação entre as variáveis explicativas e resposta e de prever um novo valor.
Há outros detalhes da teoria, mas, de forma geral, a regressão linear é uma metodologia que estuda a relação entre dois fenômenos. Por meio de uma fórmula, é possível compreender o efeito que a variável explicativa tem sobre a variável resposta, além de fazer previsões de novos valores.
Você pode aprofundar os conhecimentos com o curso Estatística com R: Correlação e regressão aqui na Alura. Além disso, pode usar outros conjuntos de dados como demonstrado no artigo Aplicando a regressão linear com R.
