Machine learning em educação com R
"Explique com suas palavras o que são design patterns". Com dez alunos o trabalho de avaliação é grande, mas com duas mil respostas, como no curso de Design Patterns para Bons Programadores do Alura, o desafio fica ainda mais interessante.
O Coursera tem otimizado algoritmos automatizados através de revisão dos alunos (peer review), revisões que o Alura implementou desde seu primeiro dia. Existem duas diferenças entre o sistema de peer review deles e o nosso. A primeira é a granularidade das questões: enquanto no Coursera existe um projeto a ser criado, o projeto a ser criado no Alura é quebrado em diversos exercícios. Segundo, nossos alunos podem acessar o sistema a qualquer instante do ano, quer estudar no Natal o curso de janeiro? Sem problemas. No Coursera todos os alunos fazem o curso obrigatoriamente ao mesmo tempo, permitindo que o peer review dê uma nota ao término do período do curso. No nosso caso, os alunos fazem a qualquer instante, então não existe o conceito de "término de semestre" para que possamos aplicar o algoritmo uma única vez, ele deve ser aplicado sempre.
Por outro lado, uma pesquisa sobre a análise de perguntas subjetivas é capaz de prever as notas dos alunos baseados em poucas informações que possuem sobre os mesmos em seus trabalhos de casa.

Enquanto o objetivo final pode ser uma avaliação automatizada, damos um passo por vez, tentando descobrir nesse instante o quanto um aluno se envolveu com um exercício, o quanto se dedicou ao mesmo. No nosso caso, dada a questão do curso de Design Patterns, avaliamos pouco mais de 300 respostas de alunos (das mais de 2000 que possuimos), usando o seguinte critério de avaliação:
- 1 a 4 - Errado, por exemplo: "Design Patterns é escrever código bonito"
- 5 - Certo, sem esforço extra, por exemplo: "Design Pattern é um padrão de solução de um problema recorrente."
- 6 a 10 - Certo, com esforço extra, por exemplo: "Design Pattern é um padrão de solução de um problema recorrente, onde tentamos analisar diversas características do código, como coesão, acoplamento, facilidade de manutenção etc."
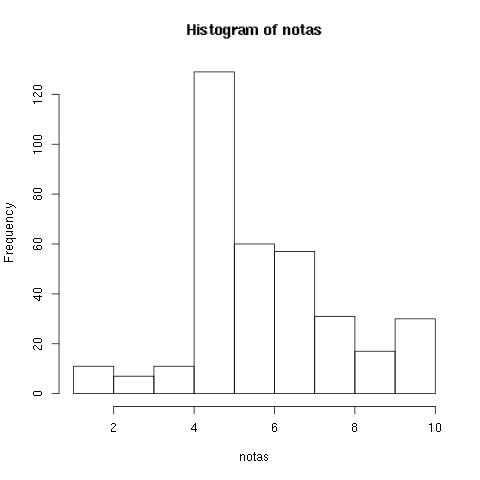
Utilizando o código em R a seguir carregamos a lista de exercícios avaliados e vemos o histograma das notas:
mainData = read.table("/tmp/table\_AnswerSizeExtractor\_154.data", header=TRUE); summary(mainData) hist(mainData$nota, main = "Histograma de notas") 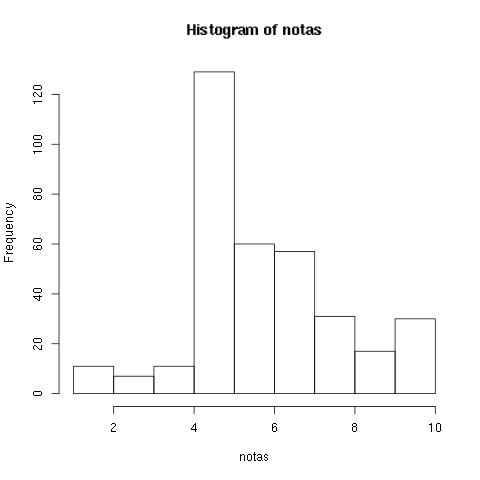 Histograma de um sample de 300 notasA maior parte dos alunos dá a resposta exata e suficiente. Isso significa que numa prova tradicional a maior parte dos alunos tiraria uma nota 10. Como assim?
Uma vez que eles assistiram a aula e levaram o tempo desejado para continuar, eles sabem o que estão falando. Uma menor parte corre atrás de explicações mais complexas ou pesquisar algo ainda fora da aula, e a esmagadora minoria erra o que foi mostrado durante a aula. Este é um padrão muito diferente do que vemos em salas de aula tradicionais: no mundo online assíncrono do Alura, o aluno responde o exercício quando está seguro, portanto ele tem o tempo que quiser para aprender, ao invés de ser pressionado por responder algo quando não está preparado.
O gráfico parece indicar que o exercício é capaz de dizer algo sobre quem está se dedicando ainda além do requerido pelo curso, "estes alunos se esforçaram bastante mesmo". E essa será a pergunta que tentaremos responder automaticamente, não a nota do aluno em relação a corretude, mas em relação ao esforço.
Separaremos somente 80% dos dados para análise, o resto será usado numa fase chamada cross validation, que não será analisada ainda neste post:
set.seed(1235); mainSelection <- createDataPartition(y=mainData$nota, p =0.80, list = FALSE); exercises <- mainData```mainSelection,
Usamos pseudo aleatorização (set.seed(1235);) pois queremos replicar o experimento e obter os mesmos resultados. Quando for de interesse rodar o experimento diversas vezes, podemos tirar a característica pseudo dela (o seed):
newOrder = sample(dim(exercises)\[1\]) newOrdered <- exercises```newOrder,
Com o newOrdered em mãos, defino que quero utilizar só as primeiras 200 notas e o método de treino será o generalized linear model (glm) da estatística, um modelo de regressão linear que não se aplica necessariamente a distribuições normais:
n = 200 method = "glm" usedData = newOrdered Estraímos as 200 primeiras notas e quebramos nossas notas em dois grupos: o de treino (60% daqueles 80% originais) e o de teste (os restantes 40% dos 80% originais):
exercises\_ <- usedData```seq(1,n),
delta = 0.6 training = exercises\_```seq(1,n\*delta),-c(1)
testing = exercises\_```seq(n\*delta+1,n),-c(1)
Quais os dados que podemos nos basear para o algoritmo de machine learning? Eles serão nossas features iniciais. Tentamos diversos dados inicialmente, como o número de caracteres existentes na resposta, o número de palavras, a existência das palavras mais frequentes, a existência de palavras chave para o curso, a hora em que o exercício foi feito e quanto tempo após o início do curso o exercício foi terminado.
Plotamos algumas dessas features aqui, uma em função da outra:
nota <- which(names(training)=="nota") all\_but\_nota <- names(training)```c(-nota)
featurePlot(x=training```,c(all\_but\_nota)
, y = training$nota, plot = "pairs")  Relação entre algumas featuresCada quadrado do meio indica uma variável: tamanho do texto, hora do dia, a palavra acoplamento, o tempo para responder e a nota. O featurePlot imprime o gráfico entre todas essas variáveis. A correlação entre tamanho do texto e nota, tempo de resposta e nota e até mesmo hora e nota são visíveis. Interessante que a hora parece ter uma relação inversa: quanto mais cedo no dia, menos a pessoa está disposta a pesquisar.
Dentre essas variáveis podemos verificar se alguma delas possui um espectro muito pequeno de valores, o que dificultaria prever algo. Por exemplo, se todos os samples fossem as 2 horas da tarde, seria inútil (e provavelmente só adicionaria ruído) utilizar essa variável:
nsv <- nearZeroVar(training, saveMetrics=TRUE)
freqRatio percentUnique zeroVar nzv text 1.000000 79.166667 FALSE FALSE hora 1.000000 16.666667 FALSE FALSE acoplamento 23.000000 1.666667 FALSE TRUE timeFromEnrollToAnswer 2.466667 42.500000 FALSE FALSE nota 1.708333 7.500000 FALSE FALSE Todas as variáveis que citamos tem um valor interessante, exceto a existência da palavra acoplamento, algo muito raro. Portanto talvez seja interessante remover essa feature em favor de um algoritmo que será rodado somente com as outras: code linhas\_a\_sair <- -which(nsv,c("nzv")
) palavras_a_ficar <- row.names(nsvlinhas\_a\_sair, ) training <- training,palavras_a_ficar
testing <- testing```,palavras_a_ficar
Também queremos verificar que as variáveis não tem uma correlação muito alta (assumimos > 0.8). Nesse caso seria interessante descartar uma delas ou refazer nosso modelo (usando algo como PCA) para encontrar dimensões melhores de estudo, uma vez que as variáveis não são linearmente independentes:
```code
M <- abs(cor(training```,-dim(training)\[2
\])) diag(M) <- 0 which(M > 0.8,arr.ind=T)
text hora timeFromEnrollToAnswer text 0.0000000 0.19594511 0.10875271 hora 0.1959451 0.00000000 0.08017649 timeFromEnrollToAnswer 0.1087527 0.08017649 0.00000000 Para nossas três variáveis que sobraram, a correlação está adequada. Quando rodamos com o tamanho da resposta e quantidade de palavras, existia uma correlação muito alta (óbvio). Além disso, quando verificamos frequência de palavras, a palavra "que" estava ligada, claro. Quanto mais "que", maior sua resposta.
Removidos os que não desejavamos, podemos treinar nosso modelo de machine learning, com um pré processamento que centraliza e reescala nossos valores:
modelFit <- train(nota ~.,data=training, method=method, preProcess=c("center","scale")) Prever e calcular o resultado da diferença:
pred <- predict(modelFit, testing) comparisons <- abs(testing$nota-pred) summary(comparisons)
\> Min. 1st Qu. Median Mean 3rd Qu. Max. > 0.01024 0.23900 0.57970 1.10300 1.52300 8.61300 Em média, a nota calculada pelo algoritmo desvia 1 ponto do valor atribuído pelo ser humano. A mediana do erro é de 0.6 pontos. 75% das notas estimadas pelo algoritmo tem um erro entre 0.23 e 1.5. Vamos ver o que foi previsto com calma?
> pred \[1\] 6.527028 9.626470 5.694002 5.814535 5.030890 7.275366 5.630889 6.775342 5.537545 5.246055 6.068363 6.912022 5.145390 4.784051 5.049604 5.819568 4.406784 5.157855 6.074759 ```20
5.591098 5.824325 6.566863 4.700698 8.200179 5.211092 5.900635 6.000707 5.639649 6.498073 5.098066 7.580328 6.135108 4.820109 6.531620 5.960835 5.160616 8.092542 12.049525 ```39
5.520743 5.932307 6.324941 4.784416 5.449062 5.658569 5.207220 7.585563 4.892635 11.588570 5.177215 6.538558 6.200410 6.878362 4.951812 5.401059 5.750975 5.123147 5.894604 ```58
5.616458 5.330652 5.665658 5.282087 5.217718 5.994488 4.838205 6.595271 4.476432 10.757157 6.010240 5.684189 6.076727 5.863875 5.431632 7.148311 4.827766 8.504189 9.893905 ```77
7.235389 6.076417 \*\*18.613354\*\* 4.958207 Nota 18? Opa, o problema de funções lineares é que elas explodem, temos que limitar nossas previsões. A maneira mais simples será limitar a nota máxima em 10 e a mínima em 0:
pred <- pmin(pred,10) pred <- pmax(pred,0) comparisons <- abs(testing$nota-pred) summary(comparisons)
\> Min. 1st Qu. Median Mean 3rd Qu. Max. > 0.0000 0.2084 0.5589 0.9407 1.2660 3.7840 Melhorou mas com esses erros o algoritmo pode não parecer interessante para dizer a nota do aluno (afinal, o número de features é pequeno e muito simples), mas ele serve muito bem para dizer se o aluno se esforçou mais do que o necessário, se esforçou o suficiente ou errou o exercício.
Mas treinarmos 200 alunos é complicado, qual seria o resultado se treinássemos somente 20 alunos? 100 alunos? Extraímos uma função para executar entre start e o máximo de respostas que temos em mãos:
mean\_comparisons <- function(start, delta, data, method) { res = seq(start, dim(exercises)\[1\], delta) values <- matrix(nrow=length(res), ncol=2) for (i in 1:length(res) ) { n = res\[i\] values```i,1
= n values```i,2
= median(calculate\_comparisons(n, data, method=method)) } return (values) } Rodamos a partir dos 20:
all\_attempts = mean\_comparisons(start = 20, delta = 1, data = newOrdered, method = "glm") summary(all\_attempts```,c(2)
) O resultado?
Min. 1st Qu. Median Mean 3rd Qu. Max. 0.2034 0.5585 0.6050 0.6270 0.6856 1.1410 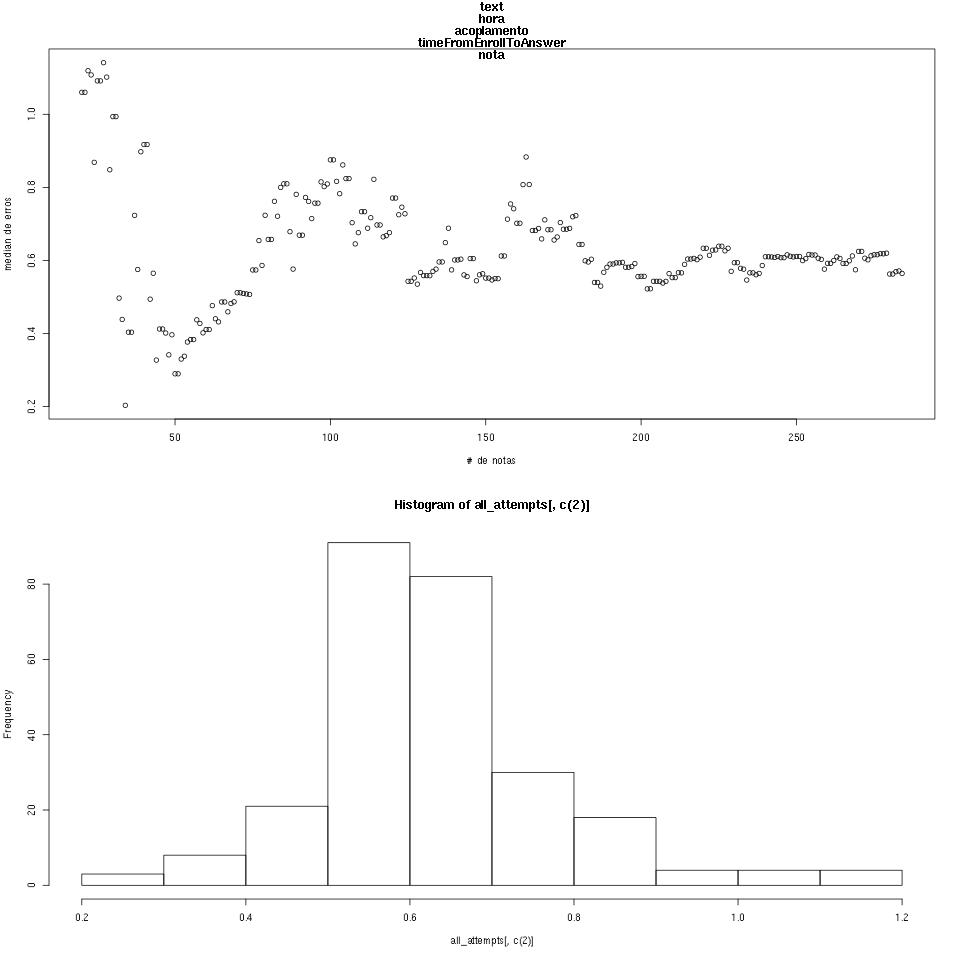 Erros em funcão de samples e distribuição dos errosO summary não nos diz muito: a média e a mediana do erro é interessante. Mas o gráfico mostra que, na prática (quando no futuro utilizarmos o cross validation) temos o que desejamos: o valor da aplicação no dia a dia. Mas saber que o erro estabiliza a medida que o treino aumenta é suficiente, e saber que o erro se mantem em uma faixa boa o suficiente para dizer quem está indo além pode ser adequado para dar algo a mais para este alguém: o famoso carimbo de estrela que ganhávamos quando éramos criança na escola, nos esforçamos mais do que o necessário.
Próximos desafios? E para outros exercícios? Essas features serão suficientes? Quais features podemos usar? E em um projeto maior, como um que pede para criar um projeto inteiro e nos dizer o que achou sobre o processo de criação?