Função de autocorrelação

Quem estuda data science já deve ter ouvido falar que duas variáveis estão correlacionadas ou que correlação não implica em causalidade. Mas o que é e para que serve essa tal de correlação?
Correlação e causalidade
O termo correlação é normalmente mencionado quando estamos tentando determinar uma relação de dependência entre duas variáveis. Por exemplo: Se diminuirmos o preço dos livros em e-commerce, as vendas aumentarão? Em que medida essas duas grandezas estão relacionadas?
Vamos tomar como exemplo essa base de dados, em que uma das variáveis é o ano, outra variável é o número de piratas e a última é a temperatura média global. Ao construirmos o gráfico dessa base de dados vemos que conforme o número de piratas foi diminuindo no eixo x no decorrer das décadas a temperatura média global foi aumentando. Isso quer dizer que as duas informações estão negativamente (ou inversamente) correlacionadas; ou seja, o número de piratas diminuiu e a temperatura aumentou.
As variáveis estariam positivamente correlacionadas se o número de piratas aumentasse e a temperatura também.
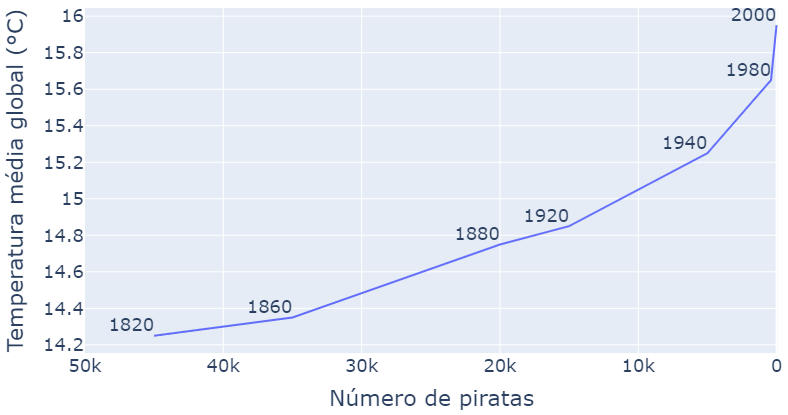
Porém, apesar dessa correlação existir temos que usar o nosso bom senso e as pesquisas científicas existentes para contextualizar os dados. A presença de piratas não resfria ou aquece o planeta e por isso o aumento do seu número não implica em diminuição ou aumento de temperatura. Ou seja, esta correlação não implica em causalidade.

Coeficiente de correlação
Mas será que há alguma forma de sabermos que existe correlação entre duas variáveis sem a necessidade de construirmos um gráfico? Os coeficientes de correlação são utilizados com este intuito. Existem muitos tipos de coeficientes de correlação, mas o mais popular é o coeficiente de Pearson (r) comumente utilizado em regressão linear.
Outro nome que damos para as correlações positivas e negativas são respectivamente: as diretas(quando as duas grandezas aumentam ao mesmo tempo) e as indiretas(quando uma grandeza aumenta e a outra diminui).
Quando encontramos o valor de “r” podemos afirmar que a correlação de fato existe. Quando o valor de “r” for positivo teremos uma correlação direta; já quando ele for negativo, teremos uma indireta.
Quando calculamos o valor de r, podemos classificar o grau de correlação dessa maneira:
| Valor de r (+ ou -) | Interpretação |
|---|---|
| 0,00 a 0,19 | Uma correlação bem fraca |
| 0,20 a 0,39 | Uma correlação fraca |
| 0,40 a 0,69 | Uma correlação moderada |
| 0,70 a 0,89 | Uma correlação forte |
| 0,90 a 1,00 | Uma correlação muito forte |
Na imagem vemos que o coeficiente de Pearson retorna uma correlação nula quando não existe correlação. Já quando a correlação existe e é positiva o coeficiente é alto e positivo. O mesmo coeficiente é negativo quando temos uma correlação alta e negativa. Isso quer dizer que valores negativos também indicam alta correlação, só que uma correlação negativa. O coeficiente de correlação de Pearson pode variar de -1 até 1.
Quando tivermos uma correlação alta e positiva teremos uma função como essa:
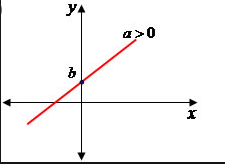
Se o r for nulo, não há correlação.
Já se o r for negativo, a correlação é indireta:
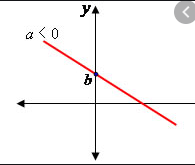
A fórmula matemática para calcularmos o coeficiente "r" é a seguinte:
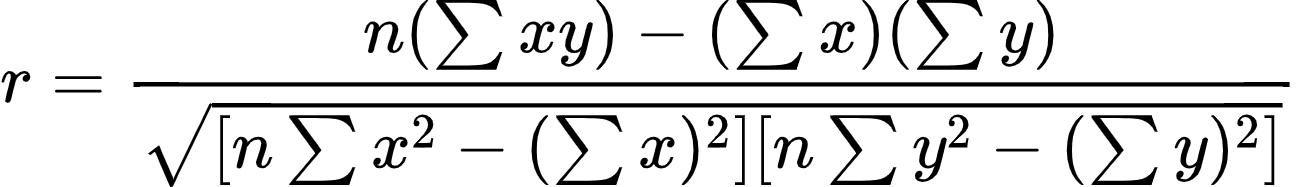
Claro que na prática não vamos usar essa fórmula toda vez que quisermos encontrar a correlação entre duas grandezas; no entanto, é interessante que você conheça e saiba de onde vem esse coeficiente, pois isso te dará uma maior firmeza e embasamento na hora que for utilizar esses conhecimentos para fazer a análise.
Função de autocorrelação
A autocorrelação é a correlação de uma variável com ela mesma. Só que a correlação de uma variável com ela mesma é sempre igual a 1 já que temos uma correlação perfeita.
Mas então, por que faríamos uma correlação de algo com ele mesmo? Se temos apenas um pedaço da série observada, como podemos afirmar com certeza que toda a observação tem um mesmo comportamento, como uma sazonalidade por exemplo? Se aplicarmos a correlação da variável com ela mesma e obtermos um valor alto, próximo de 1, indicará que temos um comportamento parecido com o do trecho observado ao longo de toda a observação.
Vamos dar uma olhada na figura abaixo:
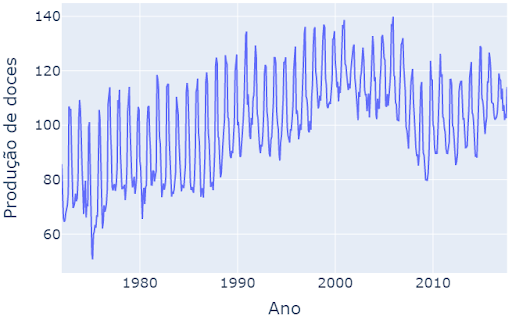
Nessa figura vemos um exemplo de série temporal, um gráfico onde uma variável está sendo mostrada no decorrer do tempo. Nesse exemplo de série temporal temos a produção de doces no decorrer do tempo. Ainda nesse gráfico conseguimos observar que os valores aumentam e depois diminuem em alguns meses do ano.
Para então termos certeza que esse comportamento não é apenas algo que aconteceu nesse determinado período observado, ou seja se trata de um evento que se repete periodicamente, podemos aplicar a função de autocorrelação. Para isso, vamos utilizar a função “CORREL” do google Sheets; porém, vamos criar um lag, ou seja, vamos comparando, deslocando o intervalo de comparação como mostramos na tabela abaixo:
| LAG | Função de autocorrelação | Comando utilizado |
|---|---|---|
| 0 | 1 | =CORREL(B$2:B549;B2:B$549) |
| 1 | 0,8750030401 | =CORREL(B$2:B548;B3:B$549) |
| 2 | 0,6854736714 | =CORREL(B$2:B547;B4:B$549) |
| 3 | 0,4560085855 | =CORREL(B$2:B546;B5:B$549) |
| 4 | 0,2899293414 | =CORREL(B$2:B545;B6:B$549) |
| 5 | 0,1758771423 | =CORREL(B$2:B544;B7:B$549) |
| 6 | 0,1438424794 | =CORREL(B$2:B543;B8:B$549) |
| 7 | 0,1607850902 | =CORREL(B$2:B542;B9:B$549) |
| 8 | 0,266215009 | =CORREL(B$2:B541;B10:B$549) |
| 9 | 0,4230717138 | =CORREL(B$2:B540;B11:B$549) |
| 10 | 0,6438300208 | =CORREL(B$2:B539;B12:B$549) |
Dessa forma percebemos que conforme variamos o intervalo de comparação(já que não é mais ela com ela mesma) vamos nos aproximando de 0. Vamos visualizar o gráfico gerado:
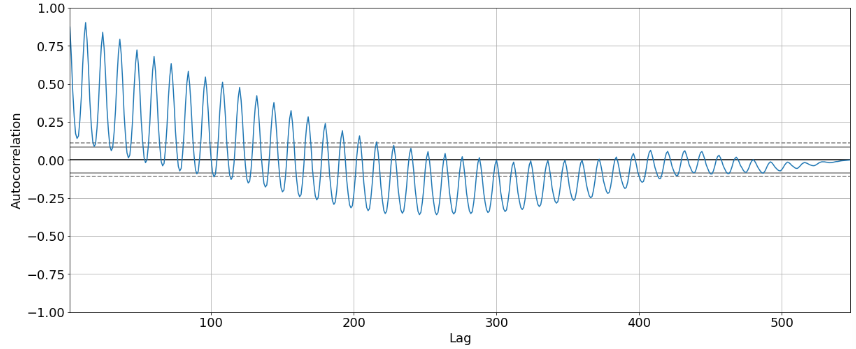
Aqui conseguimos visualizar que conforme afastamos os dados de comparação, o resultado da correlação vai se aproximando de 0. Porém, temos uma quantidade de valores bastante altos até o lag 100. Os valores altos indicam que temos alta correlação de partes distintas da série temporal. Ou seja, o evento de sobe e desce na série temporal não é algo aleatório, mas sim um mesmo evento que se repete de tempos em tempos.
Vamos analisar agora um outro conjunto de dados, dessa vez apresentando um comportamento aleatório:
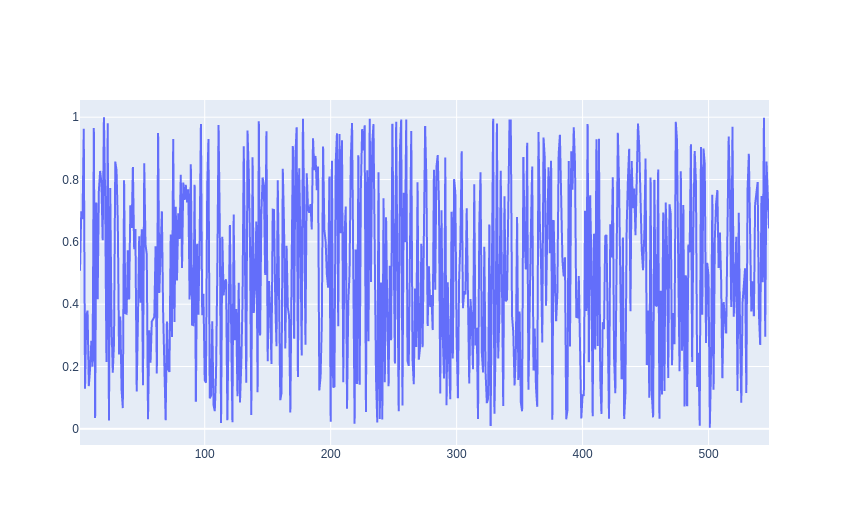
Aplicando a função de autocorrelação e gerando um gráfico obteremos a figura abaixo:
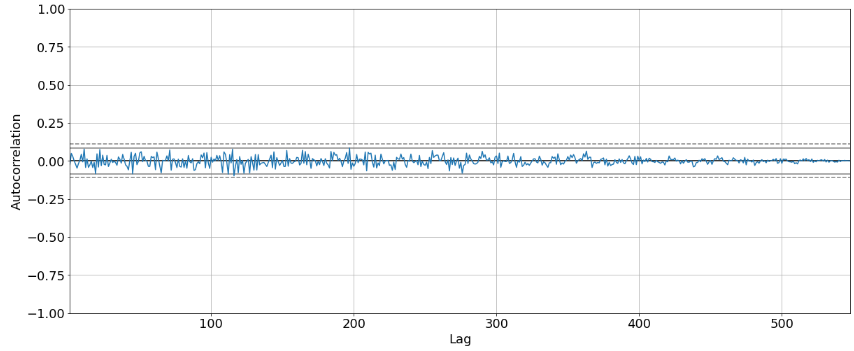
Repare como desde o início temos valores rodeando o 0. Assim percebemos que não há correlação, ou seja, esse comportamento de fato é aleatório e não tende a se repetir na distribuição inteira.
Gostou? Se você ficou com curiosidade e quer saber mais sobre a função de autocorrelação, temos esse Curso análise de série temporal: COVID-19