Correlação: compreendendo conceitos e sua aplicação

Imagine que queremos descobrir se a quantidade de horas que passamos estudando tem relação com a nossa nota em uma prova. Nesse caso, precisaríamos entender como esses dois valores estão relacionados.
Uma forma de analisar esse relacionamento é através da correlação. Através dela, somos capazes de entender como duas variáveis interagem entre si, como elas estão variando juntas.
Amplamente empregada em diversas áreas, como economia, finanças e saúde, a correlação pode te ajudar na previsão de tendências e na tomada de decisões.
Neste artigo, vamos abordar os conceitos de covariância e de correlação, compreendendo como a correlação funciona com exemplos práticos; além de entrarmos no assunto da regressão linear.
Me acompanhe durante esta leitura e vamos explorar a correlação na prática!
O que é correlação?
A correlação é uma medida estatística que descreve a relação linear entre duas variáveis.
Ela nos ajuda a entender como uma variável pode prever ou estar associada a outra. Mais especificamente, ela nos mostra a direção e a força dessa relação. As correlações podem ser positivas, negativas ou inexistentes.
| Tipo de Correlação | Descrição | Coeficiente de Correlação (r) | Exemplo |
|---|---|---|---|
| Correlação Positiva | À medida que uma variável aumenta, a outra também tende a aumentar. | Maior que 0, até 1 | Horas estudadas e nota em uma prova: Quanto mais horas uma pessoa estuda, maior tende a ser sua nota. |
| Correlação Negativa | À medida que uma variável aumenta, a outra tende a diminuir. | Menor que 0, até -1 | Horas assistindo TV e nota em uma prova: Quanto mais horas uma pessoa passa assistindo TV, menor tende a ser sua nota. |
| Correlação Inexistente | Não há uma relação linear evidente entre as variáveis. | Aproximadamente 0 | Horas estudadas e cor dos olhos: Não há uma relação linear entre essas duas variáveis. |
Nessa perspectiva, a correlação busca analisar a relação linear entre as variáveis.
A relação linear nos ajuda a visualizar e entender como uma variável pode mudar em resposta à mudança da outra, estabelecendo um vínculo direto entre elas.
Vamos então nos aprofundar e compreender como essa relação funciona no tópico a seguir.
Relação linear
A relação linear acontece quando o relacionamento entre duas variáveis cria uma linha reta.
Ela significa que quando uma variável aumenta ou diminui, a outra tende a aumentar ou diminuir de maneira proporcional.
Em um gráfico de dispersão, essa relação é visualizada como uma linha reta, como podemos conferir abaixo:
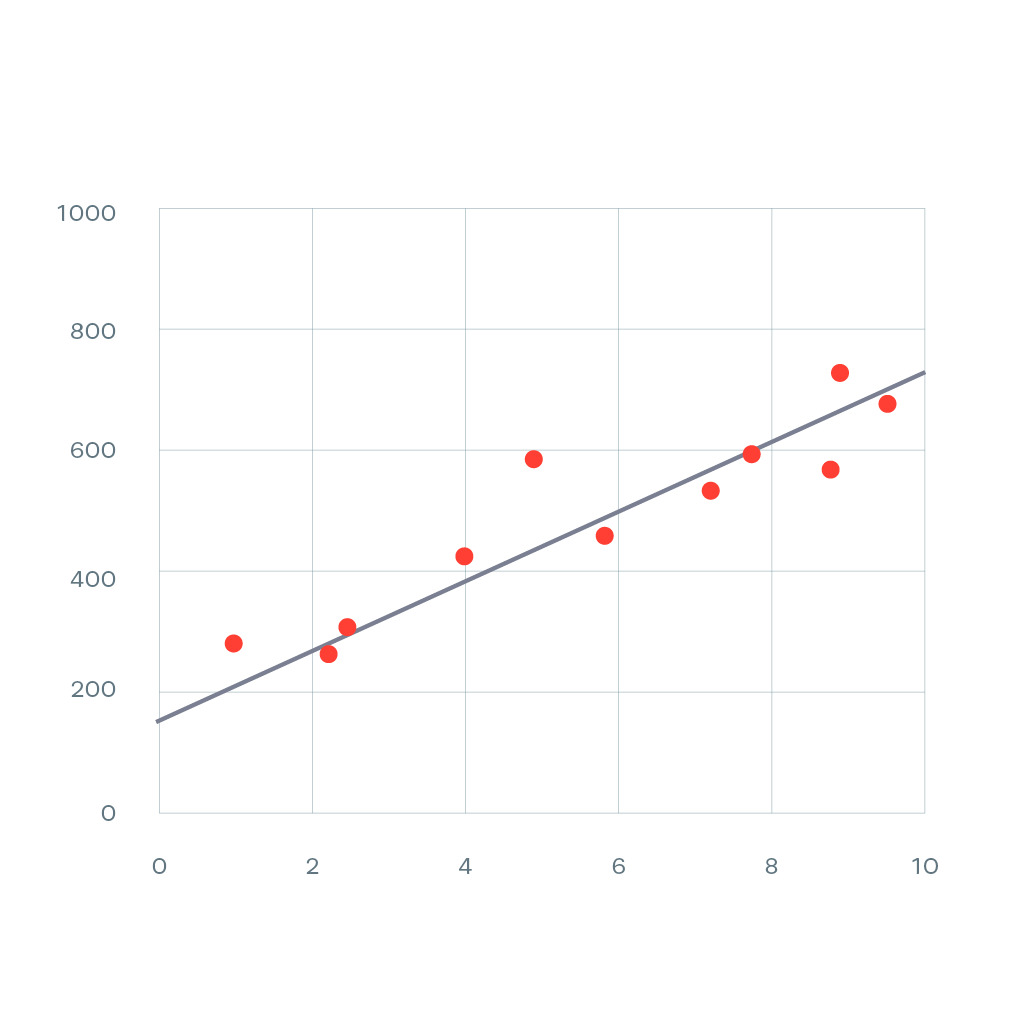
Fonte: datavizproject
Podemos representar a relação linear entre duas variáveis (x e y) matematicamente através de funções lineares.
A forma mais comum de representar uma função linear é através da seguinte função:
Y = m*X + cEm que:
Xé a variável independente, a qual já temos seu valor.Yé a variável dependente, a que queremos descobrir o valor.mrepresenta a inclinação da reta.cindica o valor de Y quando X for zero. Ela também informa por onde a reta passa no eixo Y.
Com essa função, conseguimos representar problemas do mundo real através de equações lineares.
Para tornar esse conceito mais concreto e prático, vamos retomar ao nosso exemplo do início do artigo: descobrir se a quantidade de horas que passamos estudando tem relação com a nossa nota em uma prova.
Nesse caso, teríamos o seguinte:
X: Número de horas estudadas (variável independente).Y: Nota obtida na prova (variável dependente).m: Representa a inclinação da reta, ou seja, quanto a nota tende a aumentar para cada hora adicional de estudo.c: É a nota esperada na prova se nenhuma hora de estudo foi realizada.
Agora que entendemos como uma relação linear ocorre e como podemos representá-la visual e matematicamente, como podemos descobrir se existe uma relação linear entre duas variáveis?
Para isso, precisamos entender o funcionamento da covariância.
Covariância
A covariância é uma medida que indica a existência da relação linear entre duas variáveis, assim como a direção dessa relação.
Através dela, podemos entender como os valores de duas variáveis variam de forma conjunta.
Com a covariância, a direção da relação pode ser classificada em alguns tipos, podendo assumir valores positivos, negativos ou zero:
- Positiva: Quando as variáveis tendem a aumentar juntas.
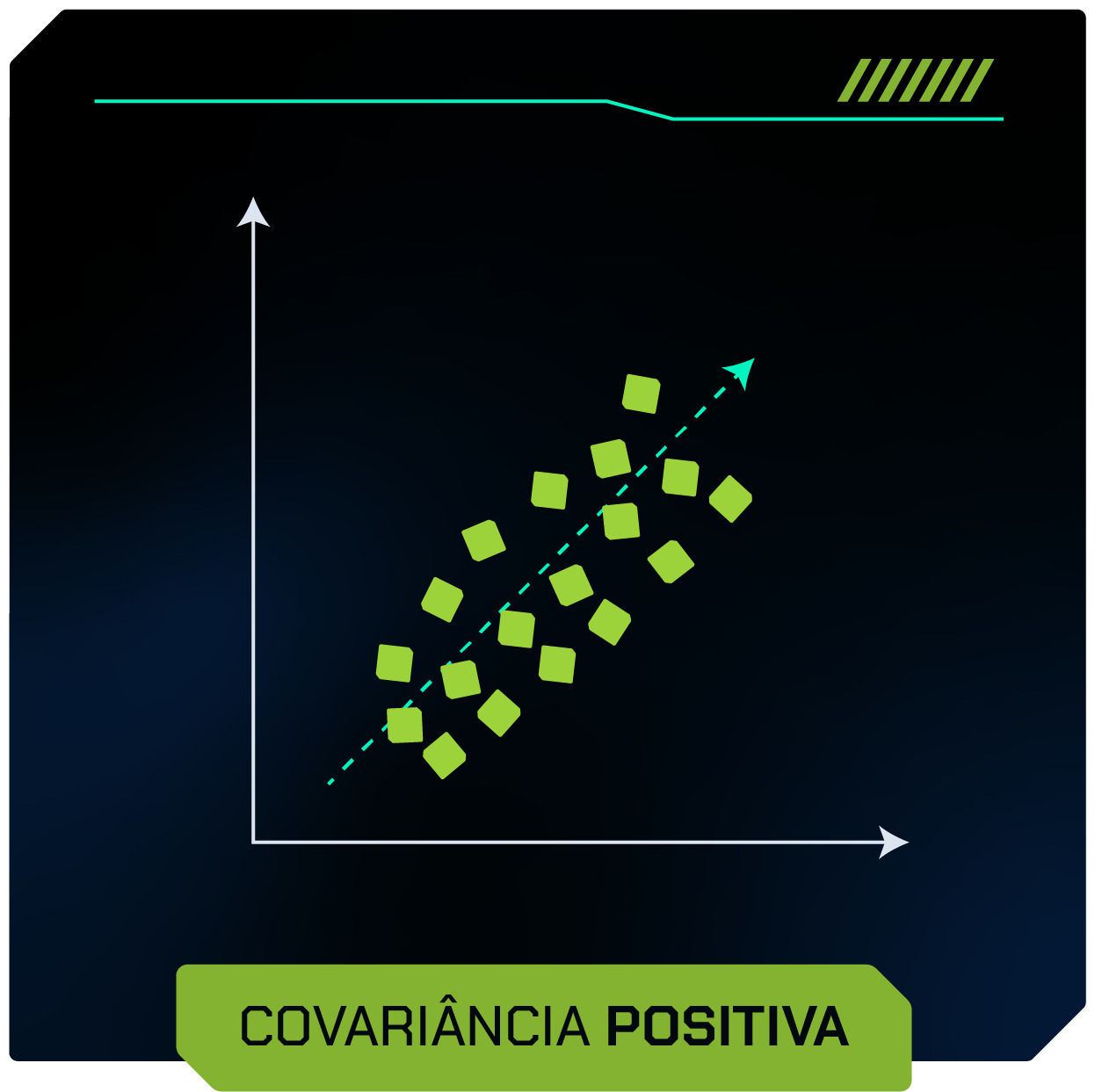
- Negativa: Quando uma variável tende a aumentar enquanto a outra tende a diminuir.
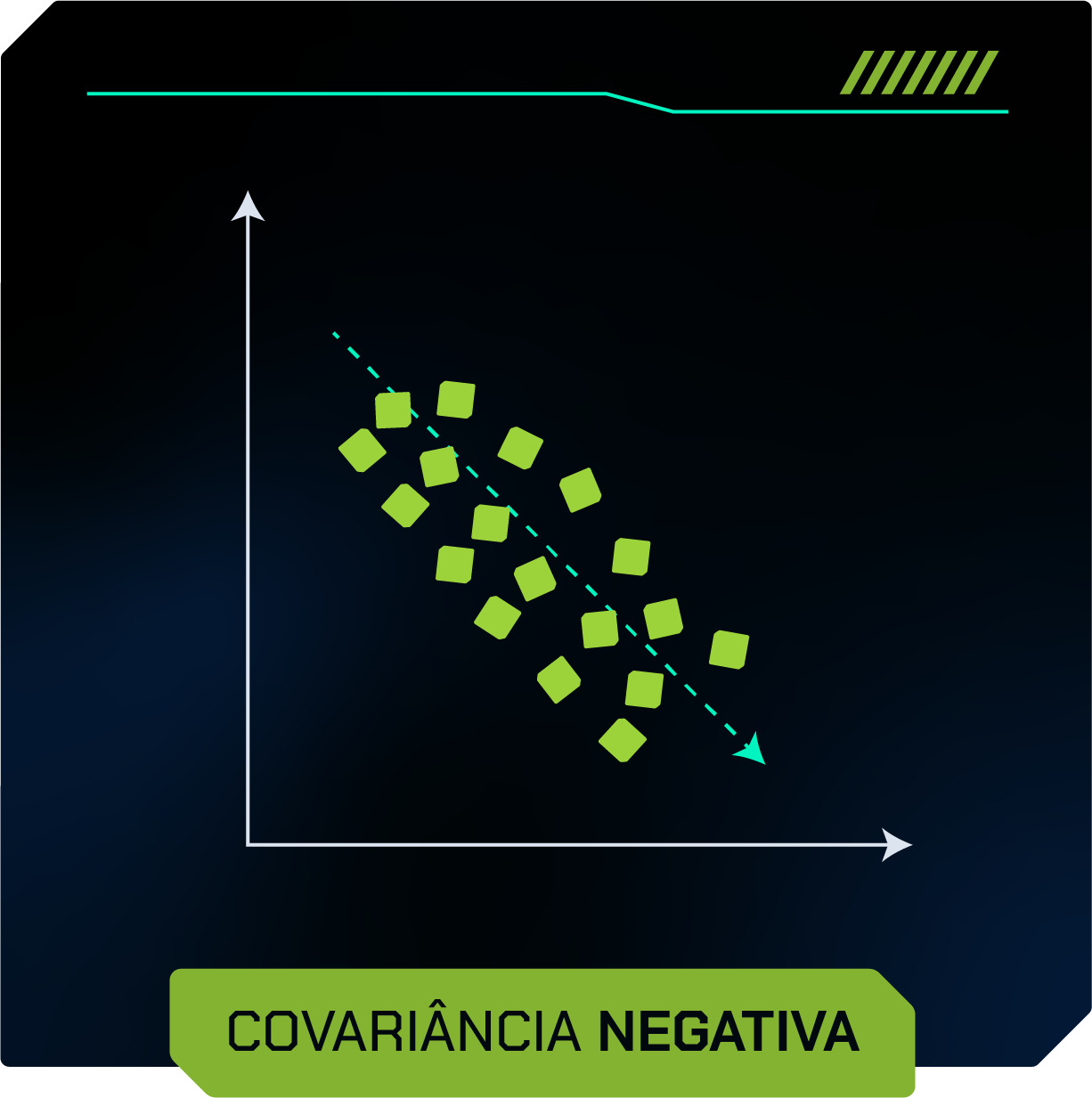
- Zero: Quando não há tendência linear entre as variáveis.
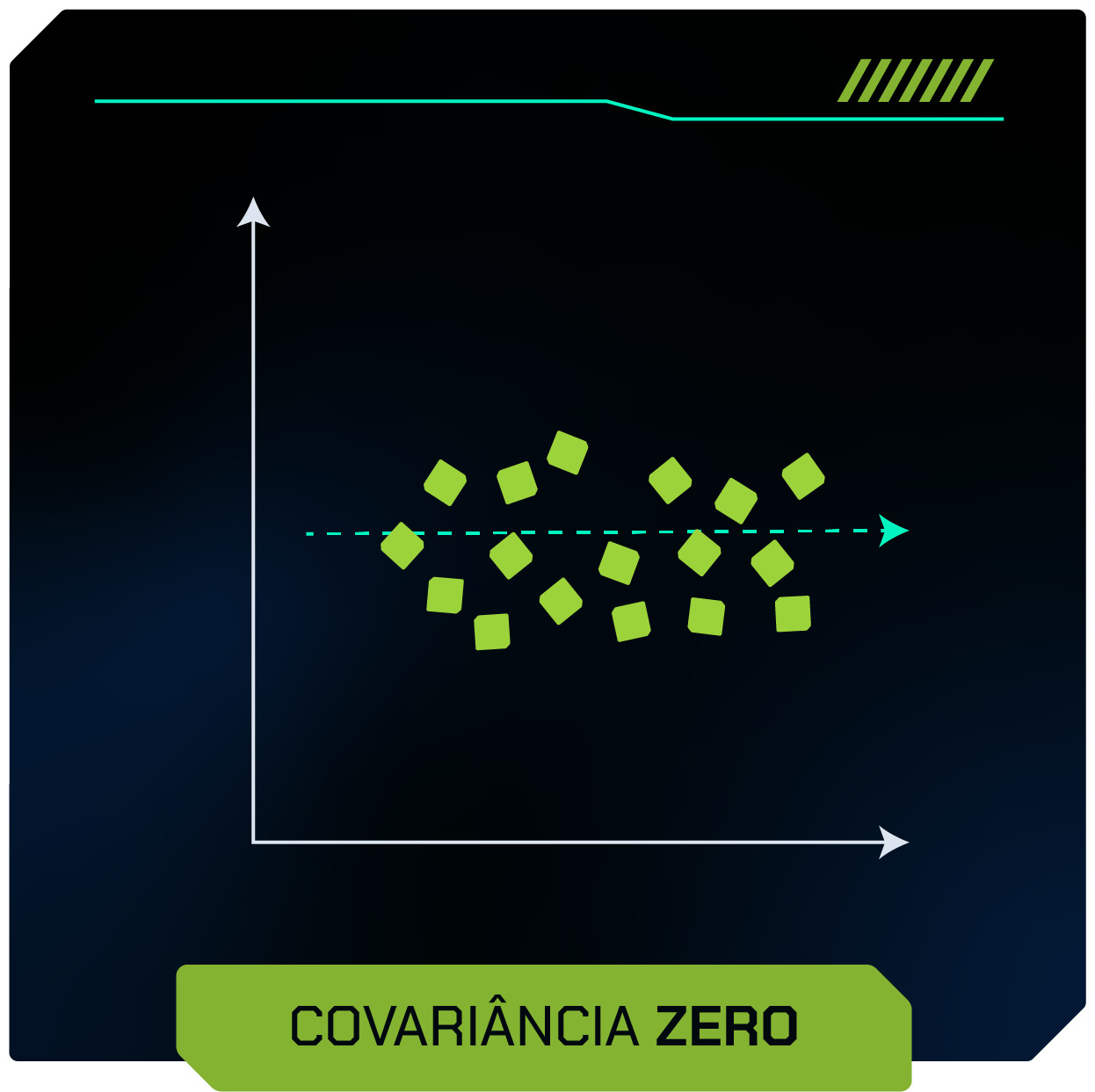
Apesar do valor gerado pela covariância nos indicar se duas variáveis estão relacionadas ou não, ele não é capaz de dizer qual a intensidade dessa relação, se é forte ou fraca.
Isso acontece porque a covariância é afetada pela unidade de medida da variável que está sendo analisada.
Na covariância, se uma unidade de medida é grande, isso não indica a força desse relacionamento. O mesmo vale para uma unidade pequena, que não quer dizer que a relação é fraca.
Para podermos obter a intensidade a partir da covariância, precisamos padronizar os seus resultados, de forma que não sejam afetados pela unidade de medida em questão.
É na correlação que essa padronização é realizada. Dessa forma, a covariância serve de base para o cálculo da correlação.

Como a correlação funciona?
Até o momento, entendemos que a covariância ajuda a descobrir a direção. Porém, ainda não conseguimos descobrir a intensidade da relação. Para avaliar tanto a direção quanto a intensidade, utilizamos a correlação.
Uma das medidas mais utilizadas para isso é o Coeficiente de Correlação de Pearson.
Coeficiente de Correlação de Pearson
O coeficiente de Pearson é calculado dividindo a covariância das variáveis pelo produto de seus desvios padrões. A fórmula é a seguinte:
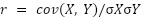
Em que:
cov(X,Y)indica a covariância entreXeY.σXeσYsão os desvios padrões deXeY, respectivamente. O valor dervaria de -1 a 1. Valores próximos a 1 indicam uma forte correlação positiva, valores próximos a -1 indicam uma forte correlação negativa, e valores próximos a 0 indicam pouca ou nenhuma correlação linear.
É através desses valores que a correlação possibilita a avaliação da intensidade da relação. Se os valores forem próximos dos extremos, 1 ou -1, a intensidade é forte.
Conforme esses valores se aproximam de zero, a intensidade vai diminuindo, até não haver correlação nenhuma. Os sinais de positivo ou negativo vão nos dizer a direção da relação.
Correlação na prática
Para ilustrar como a correlação pode ser aplicada na prática, vamos examinar com mais detalhes aquela nossa dúvida levantada no início do artigo: a relação entre o número de horas que um estudante passa estudando e suas notas escolares.
Como a nossa ideia é apenas explorar um exemplo prático, vamos utilizar dados fictícios. Temos o tempo de estudo e as notas de um grupo de estudantes para calcular a correlação entre essas variáveis.
Vamos supor que temos os seguintes dados coletados de um grupo de estudantes:
import pandas as pd
import numpy as np
# Dados fictícios de horas de estudo e notas escolares
## Simulando dados contínuos para horas de estudo e notas escolares
np.random.seed(42) # Para garantir reproducibilidade dos resultados
horas_estudo = np.random.uniform(1, 10, 100) # Gerando 100 valores entre 1 e 10 horas de estudo
notas_escolares = horas_estudo * 10 + np.random.normal(0, 5, 100) # Relação linear com ruído
## Criando DataFrame com os dados simulados
data = {'Horas de Estudo': horas_estudo,
'Notas Escolares': notas_escolares}
df = pd.DataFrame(data)
## Calculando a correlação usando Pandas
correlation = df['Horas de Estudo'].corr(df['Notas Escolares'])
print(f'Coeficiente de Correlação de Pearson: {correlation}')Neste exemplo, estamos criando um DataFrame com duas colunas: "Horas de Estudo" e "Notas Escolares". Usamos o método .corr() da biblioteca Pandas para calcular o coeficiente de correlação de Pearson entre essas duas variáveis.
Ao rodar o código acima, obtemos o coeficiente de correlação de Pearson, que indica a força e a direção da relação linear entre o tempo de estudo e as notas escolares, com o seguinte resultado:
Coeficiente de Correlação de Pearson: 0.9853662374697579
Nesse caso, o valor próximo de 1 indicaria uma forte correlação positiva, sugerindo que, conforme o número de horas de estudo aumenta, as notas escolares também aumentam.
Para verificar o resultado visualmente, vamos criar um gráfico de dispersão com as duas variáveis e traçar a linha da relação linear:
import matplotlib.pyplot as plt
import seaborn as sns
## Plotando o gráfico de dispersão
plt.figure(figsize=(10, 6))
sns.scatterplot(x='Horas de Estudo', y='Notas Escolares', data=df, color='blue', alpha=0.7)
plt.title('Relação entre Horas de Estudo e Notas Escolares')
plt.xlabel('Horas de Estudo')
plt.ylabel('Notas Escolares')
## Adicionando a linha de regressão linear
coeficiente = np.polyfit(df['Horas de Estudo'], df['Notas Escolares'], 1)
linha_regressao = np.poly1d(coeficiente)
plt.plot(df['Horas de Estudo'], linha_regressao(df['Horas de Estudo']), color='red')
plt.grid(True)
plt.tight_layout()
plt.show()Resultado do gráfico:
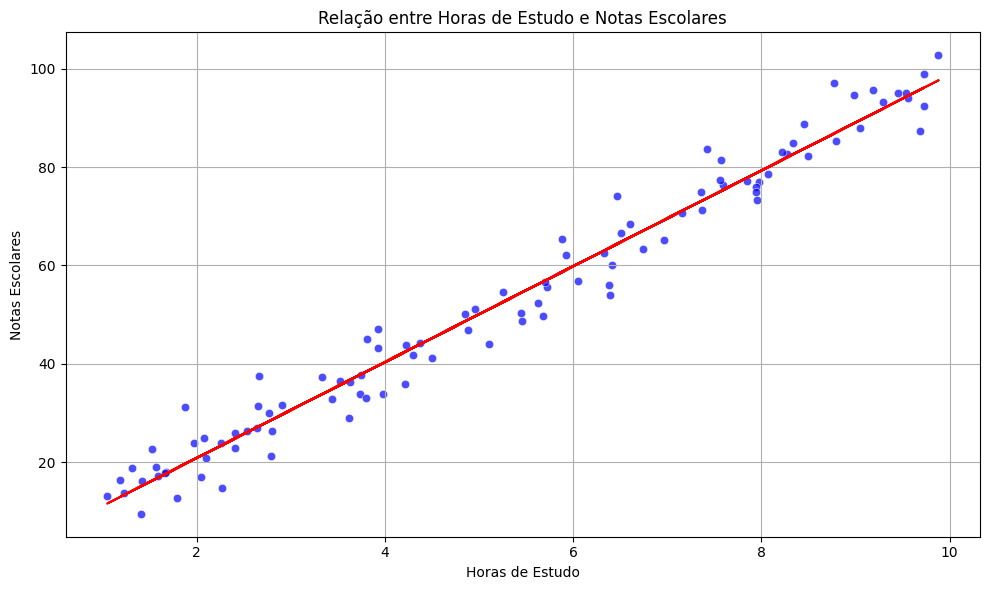
Esse gráfico permite visualizar a relação entre horas de estudo e notas escolares, destacando a tendência geral através da linha de regressão linear, enquanto os pontos representam os dados individuais simulados.
Dessa forma, esse método pode ser facilmente expandido para grandes conjuntos de dados e diferentes contextos, permitindo análises rápidas e precisas.
Correlação não é causalidade
É importante destacar que correlação não implica causalidade. Apesar de uma correlação forte entre duas variáveis indicar que elas estão associadas de alguma forma, não podemos concluir que uma variável causa diretamente a mudança na outra.
A correlação simplesmente descreve a relação entre as variáveis, mas não indica necessariamente uma relação de causa e efeito.
Por exemplo, vamos imaginar que exista uma alta correlação positiva entre o número de guarda-chuvas vendidos e o número de acidentes de trânsito em uma cidade.
Isso não implica que comprar mais guarda-chuvas cause mais acidentes de trânsito.
A correlação poderia ser explicada por outro fator, como o aumento de vendas de guarda-chuvas durante períodos chuvosos, que também pode coincidir com condições de estrada escorregadias, aumentando assim o risco de acidentes de trânsito.
Nesse caso, a correlação entre vendas de guarda-chuvas e acidentes de trânsito não estabelece causalidade direta.
Outros fatores, como condições climáticas ruins e a maneira como as pessoas dirigem, são prováveis influências simultâneas tanto nas vendas de guarda-chuvas quanto na ocorrência de acidentes de trânsito.
Regressão Linear
A regressão linear é uma técnica estatística usada para modelar o relacionamento entre uma variável dependente (Y) e uma ou mais variáveis independentes (X). A sua equação é a mesma explicada no tópico de relação linear, ou seja: Y = m*X + c.
Enquanto a correlação descreve a força e a direção do relacionamento, a regressão linear vai além ao estimar como uma variável (dependente) pode ser predita ou explicada por outra variável (independente).
A regressão linear não apenas quantifica a direção do relacionamento, mas também calcula os valores específicos da variável dependente com base na variável independente.
Durante a análise de regressão linear, os coeficientes m e c são estimados para melhor ajustar os dados observados.
A correlação pode ajudar a identificar inicialmente se existe um relacionamento linear significativo entre as variáveis antes de realizar a regressão.
Conclusão
Neste artigo, entendemos como a correlação é utilizada na prática. Durante a leitura, fomos capazes de:
- Entender como ocorre uma relação linear;
- Compreender os conceitos de covariância e de correlação;
- Explorar exemplos práticos de correlação com Python;
- Identificar como a correlação pode ser utilizada na Regressão Linear;
- Compreender que a correlação não implica causalidade.
Deseja colocar em prática os conteúdos aprendidos neste artigo?
Confira o nosso curso de Data Science: testando relações com Regressão Linear, onde você poderá contar com uma equipe especializada e altamente dedicada para fornecer conteúdos de qualidade para que você possa se desenvolver.
Até mais!
Créditos
- Conteúdo: Marcelo Cruz
- Produção técnica: Rodrigo Dias
- Produção didática: Cláudia Machado
- Designer gráfico: Alysson Manso
- Apoio: Rômulo Henrique
