Como classificar algoritmos com Big O Notation

Nesta série de artigos, abordamos a importância da análise de complexidade de algoritmos,a implementação da busca binária, a ordenação através do MergeSort e através do QuickSort. Nós sempre mencionamos a notação big O de uma forma bem abstrata e intuitiva. Que tal agora entendê-la um pouco melhor?
INTRODUÇÃO
No nosso atual contexto tecnológico, com as mais diversas máquinas e poderes de processamento e armazenamento volátil, seria inviável mensurar algoritmos apenas contando o tempo em que são executados. Então como podemos saber que um algoritmo tem um desempenho melhor que o outro?
Como abordamos nos artigos mencionados acima, uma ótima opção é calcularmos aproximadamente a quantidade de operações que o algoritmo executa. Mas que operações são essas?

Melhor, pior e caso médio
Para explicar melhor, vamos relembrar a primeira solução de busca de alunos em que utilizamos a busca linear. Decidimos que iríamos percorrer todos os alunos da lista até achar o que estamos buscando. Então vamos pensar em algumas possibilidades?
Supomos que temos a lista de alunos em ordem alfabética e estamos em busca do aluno Brendo.

Olha que coisa boa! O encontramos na primeira posição da lista e não precisamos mais percorrer-lá. Por isso este será o nosso melhor caso.
Agora precisamos ir em busca do aluno Nico.
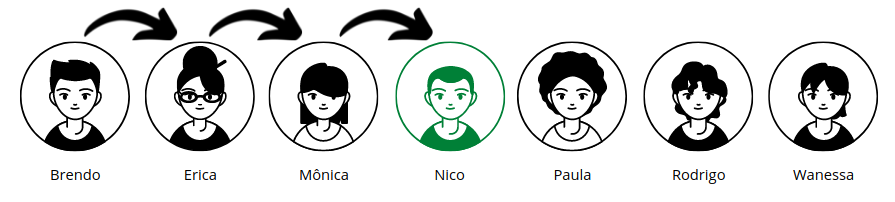
Vimos que foi necessário percorrer a metade da lista para achá-lo, então vamos considerar que este é o nosso caso médio.
Agora vamos encontrar a aluna Wanessa?
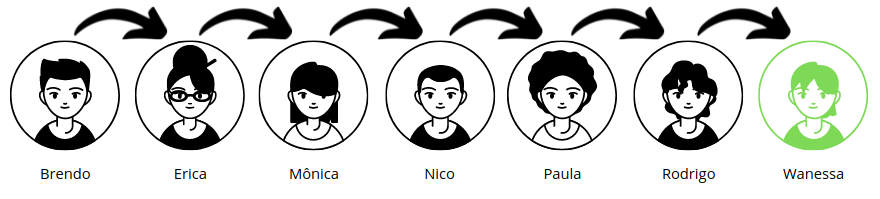
Notamos que percorremos todos os alunos até encontrá-la, então devemos considerar que este é o pior caso, certo? Certo! E onde o Big O entra nessa história? Exatamente aqui! Big O é uma notação que sempre leva em conta o pior caso.
Mas por que dividimos nossa solução em três casos se iremos utilizar apenas o pior? Guarde essa informação pois ela terá grande importância daqui a pouco!
Continuando, vamos aprofundar a análise do pior caso: nele sempre teremos que percorrer todos os alunos. E o que isso significa?
A cada aluno adicionado a nossa lista, o algoritmo executará mais uma comparação. Vamos entender isso melhor através de um gráfico?
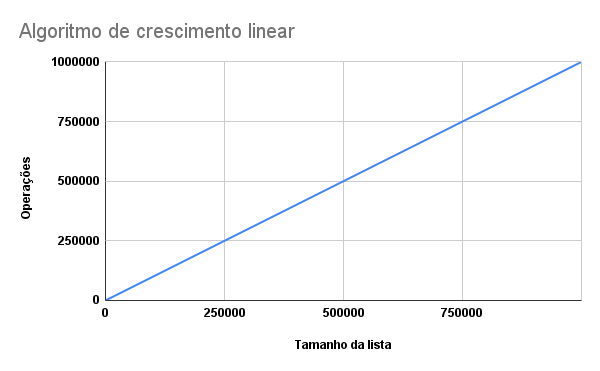
Agora fica claro que da mesma forma com que a lista cresce, o nosso algoritmo cresce de forma linear quanto a suas operações. Então podemos considerá-lo, na notação big O, como O(N).
Está na hora de analisarmos a nossa segunda solução de busca, a busca binária.
Nesta solução também devemos considerar que há uma lista ordenada e a cada comparação no meio da lista, podemos descartar a metade da lista em que o item não está.

Percebemos então que o desempenho já será bem melhor se comparado com o da busca linear, visto que nem mesmo nos piores dos casos vamos percorrer todos os itens.
Mas quão melhor é esse algoritmo? Vamos lá! Para iniciar nossa análise vamos verificar o nosso melhor caso, que ocorre quando buscamos o item do meio da lista.
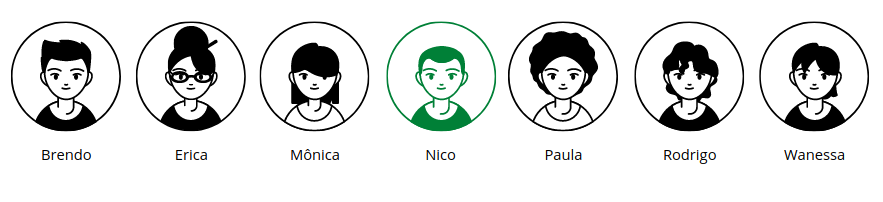
Então podemos verificar que no melhor caso, como na busca linear, a binária também se comporta como O(1).
E qual seria o pior caso? Como podemos calcular a quantidade de operações que nossa busca binária irá executar? De maneira bem intuitiva e levando em conta o que já foi informado sobre o algoritmo, vamos responder a essas duas perguntas.
Sabendo que a cada comparação podemos descartar a metade da lista, conseguimos inferir que a divisão da lista por 2 de forma sucessiva nos trará a quantidade de operações realizadas com a contagem das divisões realizadas.

Aplicando o conceito na lista acima, que continha 7 alunos, vemos que no pior caso executamos apenas 3 comparações.

Agora supomos que temos 100 alunos, então no pior dos casos executaremos 7 comparações.
Percebemos a grande diferença entre as 100 comparações que executamos no pior caso da busca linear com as 7 comparações que executamos com a busca binária. Vamos ver isso graficamente?
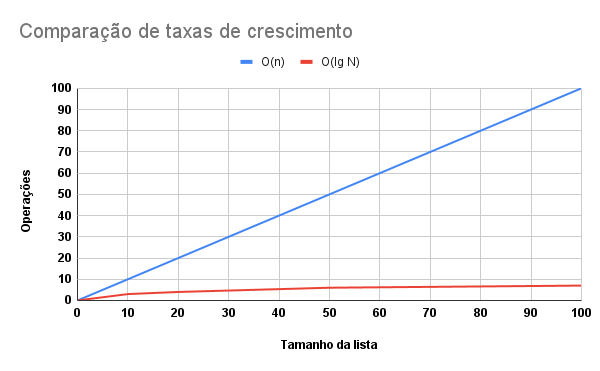
E essa diferença fica ainda mais visível quando aumentamos bastante o tamanho da lista.
Mas será que o algoritmo linear é o pior desempenho que temos em tempo de execução? Já adianto que não e podemos provar com o algoritmo de ordenação SelectionSort que explicamos no artigo de implementação do merge sort.
Mostramos que ele possui a notação assintótica de O(N²), então vamos ver o quão pior é esse algoritmo graficamente?
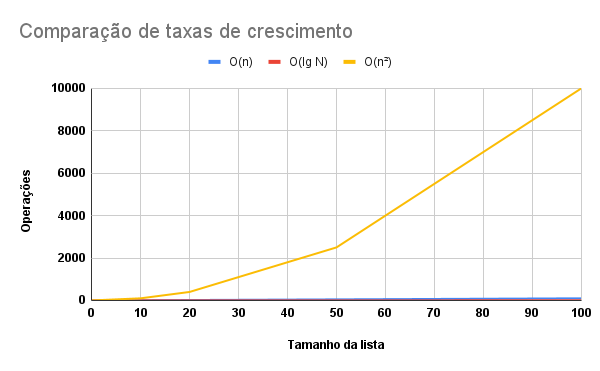
Vemos que o nosso algoritmo O(N²) ou quadrático evolui de forma exponencial em comparação aos nossos outros algoritmos que crescem discretamente no gráfico. E acredite, ainda há algoritmo piores em eficiência como os O(n³), O(2ⁿ) mas que são assuntos para outras oportunidades.
E com tudo isso, fica mais evidente a importância de conhecermos esses conceitos na hora de implementarmos os nossos programas, as nossas features.
Caso tenha seguido a trilha de artigos sobre complexidade de algoritmos, deve ter se lembrado de uma dúvida relacionada aos algoritmos de ordenação(Merge e Quick Sort): Como escolher o melhor, entre algoritmos com a mesma complexidade?
A seguir, vamos explicar mais detalhadamente quais fatores e parâmetros devemos avaliar em algoritmos com a mesma complexidade no próximo artigo da série.
Nos vemos lá!
