Análise de dados: média ou visualizar a distribuição?
Na nossa plataforma de cursos online queremos mostrar para nossos potenciais e atuais alunos e alunas o quanto as pessoas estão saindo satisfeitas após estudarem um curso. Para isso cada estudante dá uma nota entre 0 e 10, e podemos tirar a média. Por exemplo, um curso com 4 alunos que deram notas [6, 8, 9, 10] teria a média 8.25.
Ótimo, vamos calcular todas as médias de nossos cursos. Para isso usarei o Pandas em Python, e uma conexão a um banco MySQL:
sql ='''select avg(nota) as media from Registros r
where ...
group by r.curso;'''
medias = pd.read_sql(sql, conexao)
Imprimimos a média, moda e mediana:
print(f'Média: {medias.mean()}') # Média: 9.03 print(f'Moda: {medias.mode()}') # Moda: 9 print(f'Mediana: {medias.median()}') # Mediana: 9.06
Que maravilha, a nota média de nossos cursos é aproximadamente 9, assim como a nota que mais aparece (a moda, que parece não fazer sentido nenhum nessa análise) é 9, e metade dos nossos cursos (mediana) estão acima de 9.06 e metade abaixo. Mas o quanto isso diz pra mim sobre meus cursos? Ainda não muito. O desvio padrão pode nos ajudar:
print(f'Desvio padrão: {medias.std()}') # Desvio padrão: 0.33
A e o desvio padrão indicam que 95% dos nossos cursos estão entre 8.37 e 9.69. Ótimo! Sucesso para a empresa.
Mas números são difíceis de "visualizar"
Ao invés de resumir todas as informações em um único número, vamos tentar visualizar essas médias?
Usando a biblioteca seaborn (importada como `sns`) podemos plotar um "tique" para cada nota, um rugplot:
sns.rugplot(medias)
Mas como temos muitos "tiques" próximos, não conseguimos ver direito a informação. Que tal se acumularmos os tiques? Isto é, se dois cursos tem nota entre 9 e 9.1, faço uma barra de altura 2 ali. Se cinco cursos tem nota média entre 9.1 e 9.2, faço uma barra de altura 5 ali. Esse é o básico de um histograma: dividir o espaço de notas em diversos pequenos trechos e desenhar barras de acordo:
sns.distplot(medias, hist=True, kde=False)
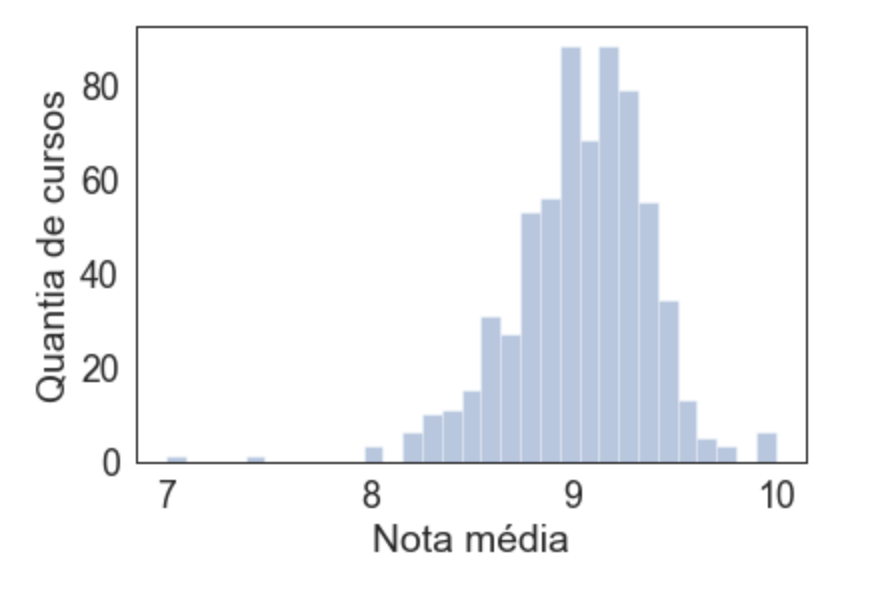
Agora sim conseguimos ver que nenhum curso tem nota média menor do que 7, e que o grande bolo de cursos está lá com notas boas entre 8.5 e 9.5. Mas podemos melhorar essa visualização, repara que dividimos em muitos pedaços pequenos, o próprio seaborn tenta adivinhar uma divisão adequada (existem algoritmos para isso), mas podemos em alguns casos que achamos interessantes forçar, como aqui quero forçar 10 espaços (bins):
sns.distplot(medias, hist=True, kde=False, bins=10)
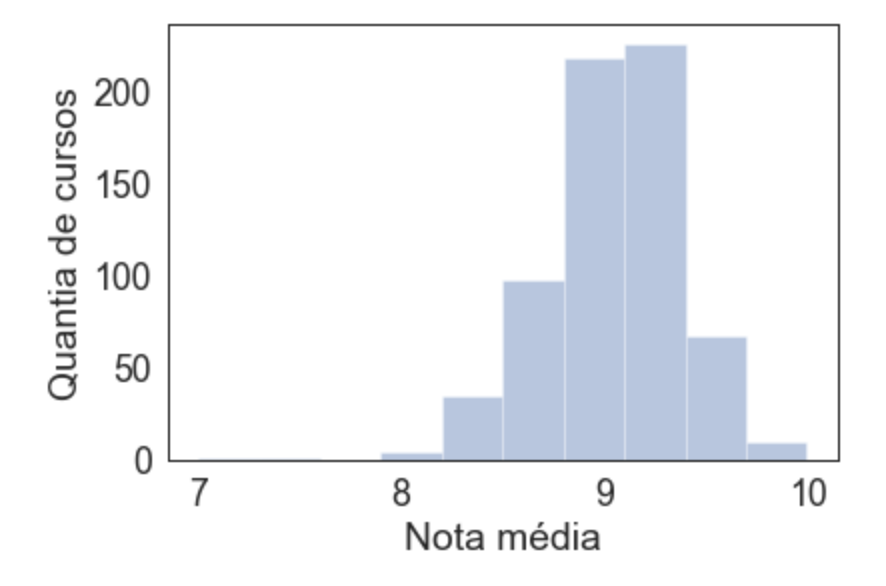
Mas repara que nossas notas médias de cada curso podem ir de 0 a 10, então podemos definir o valor mínimo e máximo, que fica ótimo para o ego, todas as notas médias acumuladas lá na direita:
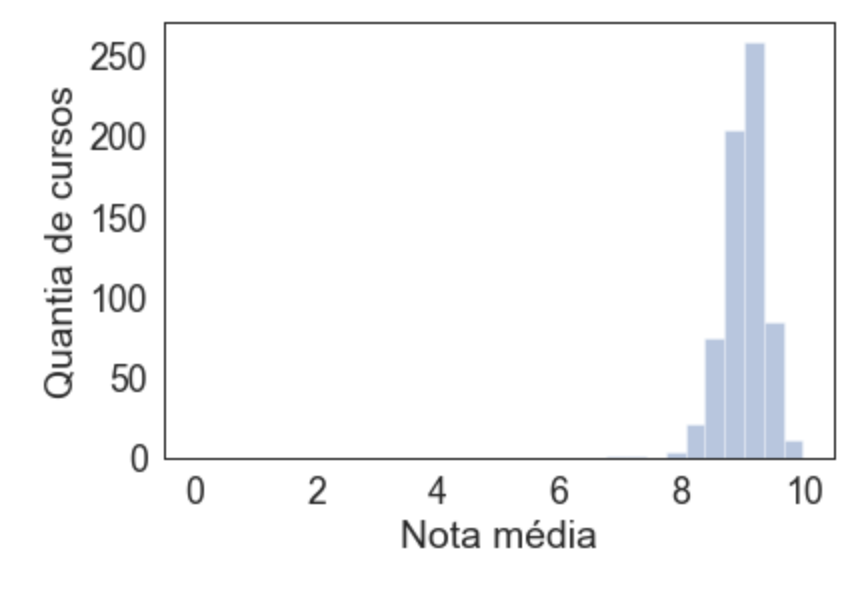
Mas não ajuda a entender a distribuição das notas né? portanto voltamos atrás e tentamos somente com o eixo x que a própria biblioteca sugere, além de 20 espaços agora:
sns.distplot(medias, hist=True, kde=False, bins=20)
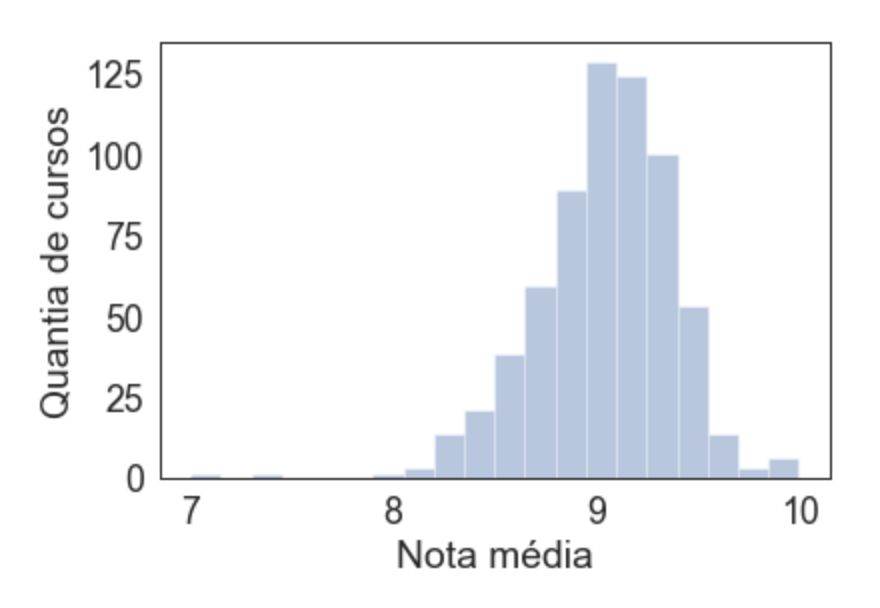
Existem tentativas de fórmula mágica para tentar descobrir um número ótimo de bins, e o padrão do seaborn tenta nos ajudar, mas repara que vai sempre depender da distribuição dos seus pontos e do que você deseja focar. No nosso caso, 20 pareceu o mais interessante.
Por mais que as barras do histograma deêm um sentido aos nossos dados, seria interessante tentar traçar uma função `f(media)` que descreva os nossos dados. A maneira mais tradicional de aproximar o histograma a uma função é através do método chamado de `kde`:
sns.distplot(medias, hist=True, kde=True, bins=20)
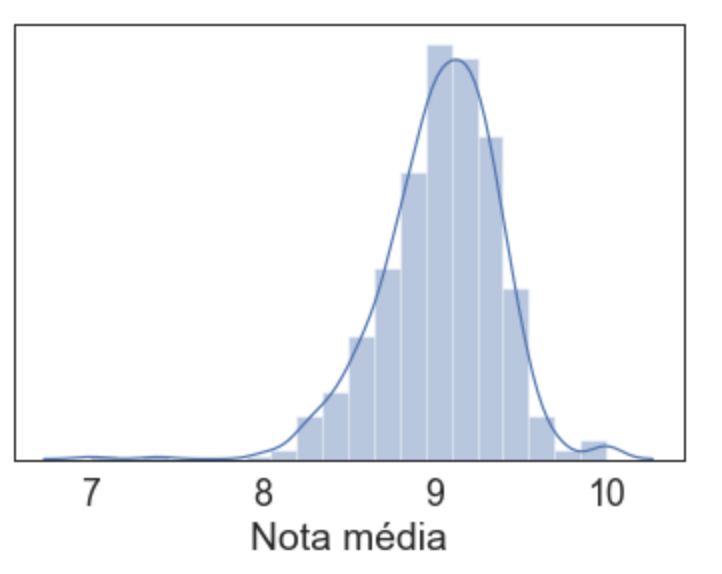
Essa função poderia ser usada para tentarmos prever a distribuição para pontos que não possuimos informação. Repara como o comportamento da distribuição dessa função se assemelha muito a uma distribuição normal (gamma):
sns.distplot(medias, fit=stats.gamma, hist=True, kde=True)
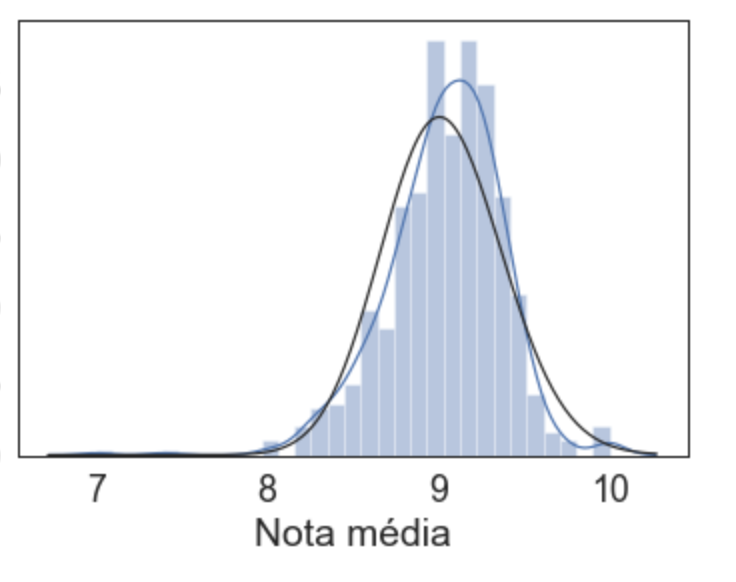
Quando seus dados se assemelham a uma normal de verdade (sem outliers, caudas tendendo a zero, assimétricas etc) aquela medida de média lá do começo e o desvio padrão podem fazer sentido, mas vamos tentar explorar um pouco mais o que conseguimos. Em geral, mais interessante que o histograma, é entender a área embaixo do histograma.
O que podemos fazer? Ao invés de plotarmos a função da distribuição - no ponto 8, médias iguais a 8, no ponto 9 médias igual a 9 - vamos acumular os valores? Isto é, no ponto 8, colocamos todas as notas menores que 8, no ponto 9, as menores do que 9. Acumulando:
sns.kdeplot(medias```'media' , cumulative=True)
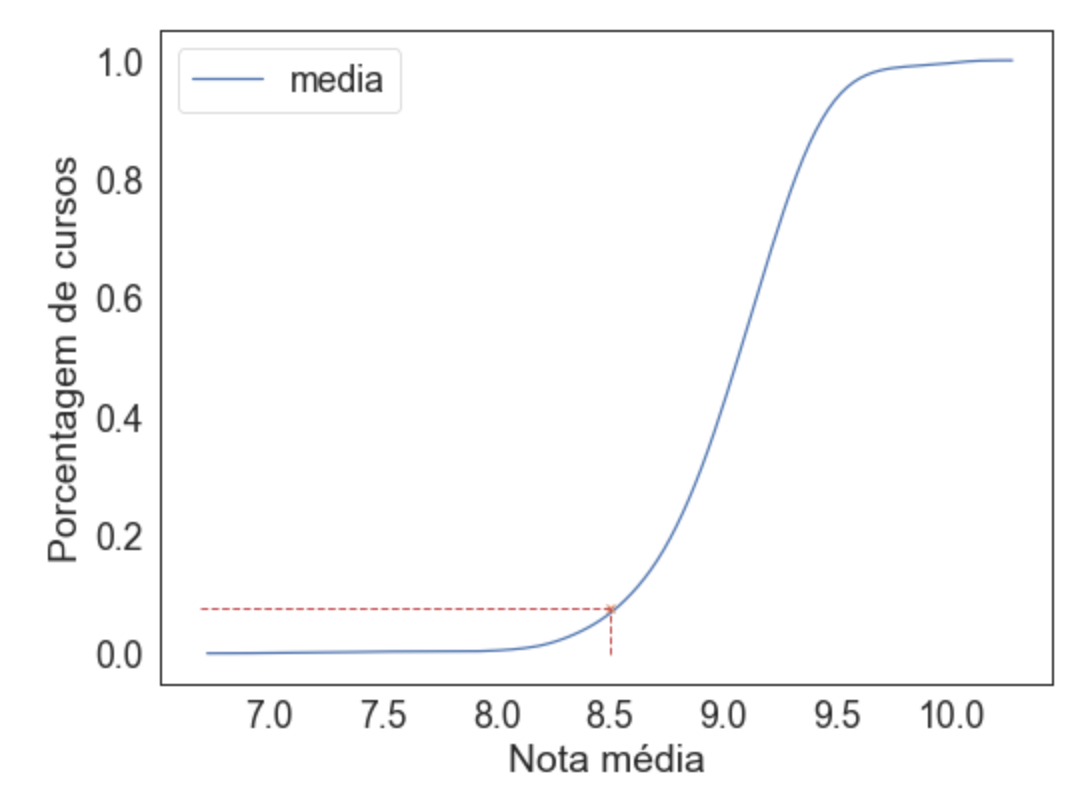
O gráfico cumulativo é muito importante. Ele mostra por exemplo, que se pegarmos a nota ~8.5, temos que menos de 8% das médias são abaixo dela. Assim como somente ~10% das médias estão acima de 9.5.
Aproveito para descrever como fazer a anotação que fiz no gráfico, plotando um pequeno `x` e duas linhas:
a4_dims = (8, 6) fig, ax = pyplot.subplots(figsize=a4_dims)
sns.kdeplot(medias```'media'
, cumulative=True, ax=ax)
ax.set_xlabel('Nota média')
ax.set_ylabel('Porcentagem de cursos')
plt.plot(8.5, 0.075, "x")
plt.plot(8.5, 8.5 ,0, 0.075
, 'r--', lw=1)
plt.plot(6.7, 8.5 ,0.075, 0.075
, 'r--', lw=1)
Três visualizações conclusivas
Mas, o mais interessante para nós será invertermos a linha de pensamento. Se rotacionarmos nosso gráfico, trocando o eixo x e y poderemos ver as porcentagens acumuladas e as notas:
sns.kdeplot(medias```'media' , cumulative=True, vertical=True)
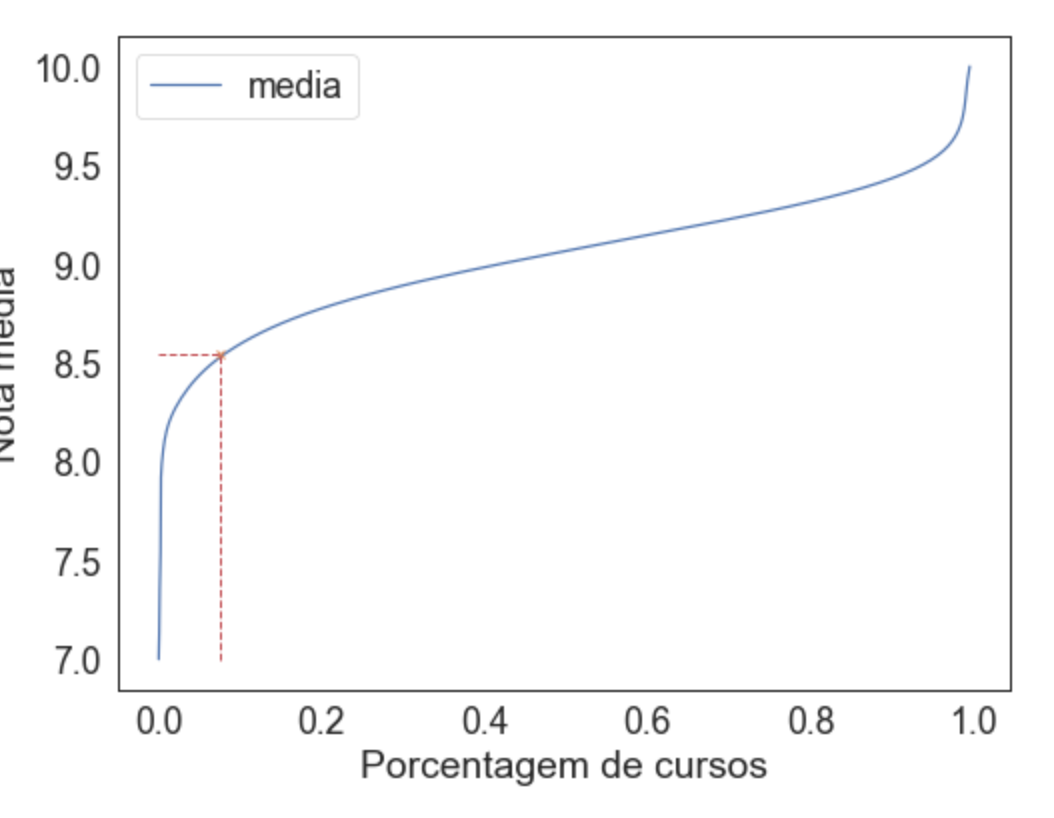
Nessa visualização rotacionada fica bem fácil de escolher uma porcentagem, por exemplo, 20% e perceber que só 20% das notas estão abaixo de 8.8.
Desafio para o/a leitor/a: qual o motivo de, a longo prazo, ser muito difícil (quase impossível) manter média máxima (10) numa avaliação?
Por fim, sem rotacionar o nosso gráfico podemos plotar o histograma cumulativo junto ao kde:
sns.distplot(medias, hist=True, kde=True, color='y', hist_kws={'cumulative': True, 'color':'g'}, kde_kws={'cumulative': True})
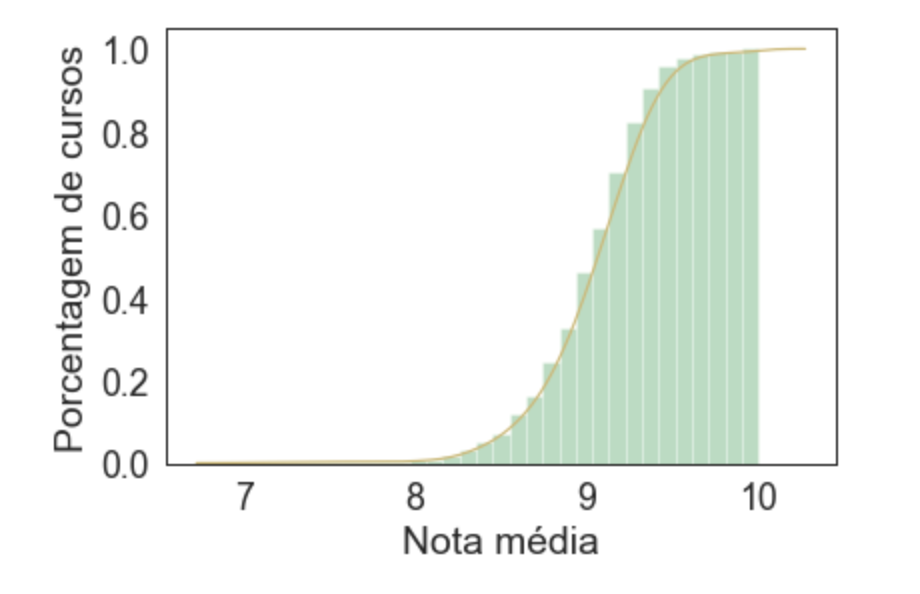
Nossos dois últimos gráficos são ferramentas ótimas para nós, como empresa, professores/as e educadores, pois indicam que os alunos em média terminam os cursos de maneira satisfatória, com notas positivas.
Mas a média não parece ajudar um ponto do aluno e da aluna. Se os top 10 cursos tem nota próximo a 10 e os bottom 10 tem nota próxima a 8, não é tão claro a diferença entre eles. E quem estuda conosco gostaria de diferenciar tais cursos claramente, para saber o que esperar de um curso com nota 8. Por isso a medida de média que estamos usando para nossos gráficos e que usávamos para mostrar a nota de nossos cursos parece não ajudar.
Visando ajudar o dia a dia de nossos alunos preferimos mudar a nota visualizada para uma outra fórmula baseada no NPS (mas não exatamente o NPS) para que a distribuição das notas ficasse mais "esticada" e nossos alunos e alunas entendam melhor que apesar de um curso ter um alto número de alunos e alunas satisfeitos, pode ou não estar no nosso top cursos. Com essa nova fórmula a distribuição é:
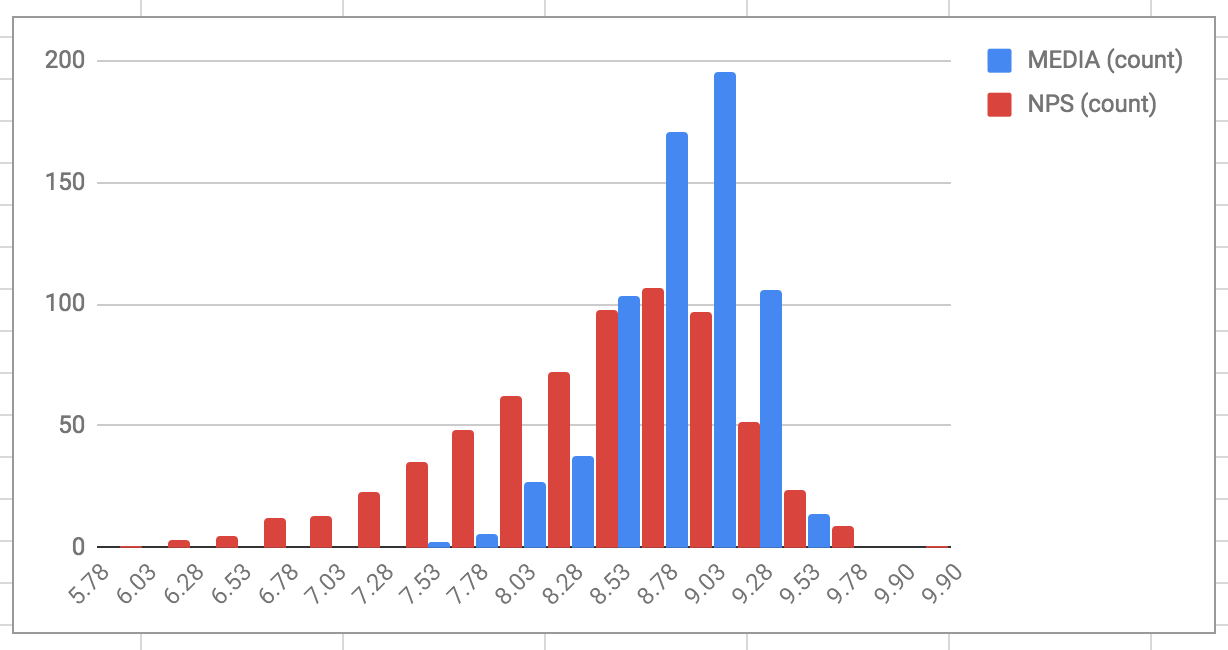
Gosto muito do resumo que o Paulo Silveira fez sobre essa decisão:
"O NPS gera números mais baixos. Pode parecer estranho, mas optamos por mostrar como média o 'NPS normalizado' por acreditar que esses números são mais coerentes à expectativa do aluno, com valores mais baixos e diferenciados em cursos que houve mais notas baixas. Caso contrário, a média simples puxava o valor para cima com facilidade, dada a esmagadora quantidade de alunos satisfeitos.".
Recursivamente, dentro da própria Alura temos um curso que ensina a trabalhar com Python e Pandas, além de diversos outros cursos para analisar nossos dados e visualizações, dando o primeiro passo na sua carreira de analista de dados.